题目内容
【题目】如图,已知△ACE是等腰直角三角形,∠ACE=90°,B点为AE上一点,△CAB经过逆时针旋转后到达△CED的位置.
问:(1)旋转中心是哪个点?旋转角是哪个角?旋转了多少度?
(2)图中哪两个三角形全等?
(3)若∠ACB=20°.则∠CDE= ,∠DEB= .
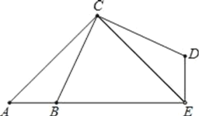
【答案】(1)C点;∠ACE或∠BCD;90度;(2)△CAB和△CED全等;(3)115°,90°.
【解析】
(1)利用旋转的定义求解;
(2)根据旋转的性质进行判断;
(3)先利用等腰直角三角形的性质得∠A=∠CEA=45°,则根据三角形内角和可计算出∠ABC=115°,再根据旋转的性质得∠CDE=∠ABC=115°,∠CED=∠A=45°,从而得到∠DEB=90°.
(1)旋转中心是C点;旋转角为∠ACE或∠BCD;旋转了90度;
(2)图中△CAB和△CED全等;
(3)∵△ACE是等腰直角三角形,∠ACE=90°,
∴∠A=∠CEA=45°.
∵∠ACB=20°,
∴∠ABC=180°﹣45°﹣20°=115°.
∵△CAB经过逆时针旋转后到达△CED的位置,
∴∠CDE=∠ABC=115°,∠CED=∠A=45°,
∴∠DEB=45°+45°=90°.
故答案为:115°,90°.

练习册系列答案
相关题目