题目内容
【题目】已知在平面直角坐标系中有两点A（0，1），B（﹣1，0），动点P在反比例函数y=
的图象上运动，当线段PA与线段PB之差的绝对值最大时，点P的坐标为_____．
【答案】（﹣1，﹣2）或（2，1）
【解析】由三角形三边关系知|PA﹣PB|≥AB知直线AB与双曲线y=
的交点即为所求点P，据此先求出直线AB解析式，继而联立反比例函数解析式求得点P的坐标．
如图，
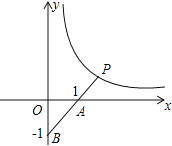
设直线AB的解析式为y=kx+b，
将A（1，0）、B（0，﹣1）代入，得：
，
解得：
，
∴直线AB的解析式为y=x﹣1，
直线AB与双曲线y=
的交点即为所求点P，此时|PA﹣PB|=AB，即线段PA与线段PB之差的绝对值取得最大值，
由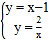
可得
或
，
∴点P的坐标为（﹣1，﹣2）或（2，1），
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
