题目内容
【题目】数学综合实践课上，老师提出问题：如图，有一张长为4dm，宽为3dm的长方形纸板，在纸板四个角剪去四个相同的小正方形，然后把四边折起来（实线为剪裁线，虚线为折叠线），做成一个无盖的长方体盒子，问小正方形的边长为多少时，盒子的体积最大？为了解决这个问题，小明同学根据学习函数的经验，进行了如下的探究：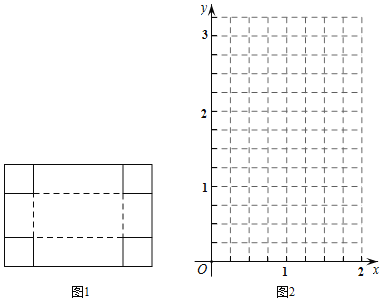
（1）设小正方形的边长为xdm，长方体体积为ydm3，根据长方体的体积公式，可以得到y与x的函数关系式是 ，其中自变量x的取值范围是 ．
（2）列出y与x的几组对应值如下表：
x/dm | … |
|
|
|
|
|
|
| 1 |
|
| … |
y/dm3 | … | 1.3 | 2.2 | 2.7 | 3.0 | 2.8 | 2.5 | 1.5 | 0.9 | … |
（注：补全表格，保留1位小数点）
（3）如图，请在平面直角坐标系中描出以补全后表格中各对对应值为坐标的点，画出该函数图象；
（4）结合函数图象回答：当小正方形的边长约为 dm时，无盖长方体盒子的体积最大，最大值约为 .
【答案】（1）y= 4x3-14x2+12x，自变量x的取值范围是0＜x＜
；（2）3，2；（3）画图见解析；（4）0.55，3.03．
【解析】
根据题意，列出y与x的函数关系式，根据盒子长宽高值为正数，求出自变量取值范围；利用图象求出盒子最大体积．
（1）由已知，y=x（4-2x）（3-2x）=4x3-14x2+12x；
故答案为：y=4x3-14x2+12x
由已知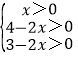
解得：0＜x＜；
∴自变量x的取值范围是0＜x＜；
（2）根据函数关系式，当x=
时，y=3；x=1时，y=2；
（3）根据（1）画出函数图象如图；
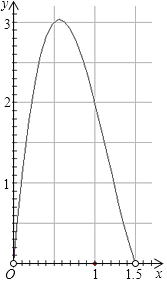
（4）根据图象，当x=0.55dm时，盒子的体积最大，最大值约为3.03dm3
练习册系列答案
相关题目
