题目内容
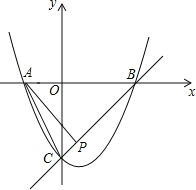
【题目】如图,在四边形ABCD中,AD∥BC,∠ADC=90°,点E是BC边上一动点,联结AE,过点E作AE的垂线交直线CD于点F.已知AD=4cm,CD=2cm,BC=5cm,设BE的长为xcm,CF的长为ycm.
小东根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行探究.
下面是小东的探究过程,请补充完整:
(1)通过取点、画图、测量,得到了x与y的几组值,如下表:
x/cm | 0 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 | 4.5 | 5 |
y/cm | 2.5 | 1.1 | 0 | 0.9 | 1.5 | 1.9 | 2 | 1.9 |
| 0.9 | 0 |
(说明:补全表格时相关数据保留一位小数)
(2)建立直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;
(3)结合画出的函数图象,解决问题:当BE=CF时,BE的长度约为 cm.

【答案】(1)1.5;(2)详见解析;(3)0.6~0.8.
【解析】
(1)根据题意作图测量即可;
(2)根据题意作图象即可;
(3)构造直线y=x与所画图象求交点即可.
(1)根据题意作图测量可得y=1.5
故答案为:1.5
(2)根据题意作图得

(3)根据题意,所画图象于直线y=x交点即为所求数值.故测量数据在0.6~0.8之间.
故答案为:0.6~0.8

【题目】一个二次函数图象上部分点的横坐标x,纵坐标y的对应值如下表:
x | … | ﹣4 | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | … |
y | … | ﹣ | 0 |
| 2 |
| 0 | m | ﹣6 | ﹣ | … |
(1)求这个二次函数的表达式;
(2)求m的值;
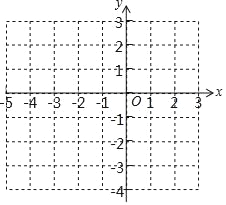
(3)在给定的直角坐标系中,画出这个函数的图象;
(4)根据图象,写出当y<0时,x的取值范围.
【题目】某校组织全校2000名学生进行了环保知识竞赛,为了解成绩的分布情况,随机抽取了部分学生的成绩(得分取整数,满分为100分),并绘制了频数分布表和频数分布直方图(不完整):
分组 | 频数 | 频率 |
50.5~60.5 | 20 | 0.05 |
60.5~70.5 | 48 | △ |
70.5~80.5 | △ | 0.20 |
80.5~90.5 | 104 | 0.26 |
90.5~100.5 | 148 | △ |
合计 | △ | 1 |
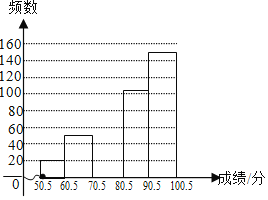
根据所给信息,回答下列问题 :
(1)补全频数分布表;
(2)补全频数分布直方图;
(3)学校将对成绩在 90.5 ~ 100.5 分之间的学生进行奖励,请你估算出全校获奖学生的人数 .