题目内容
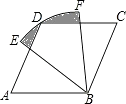
【题目】如图,四边形ABCD是平行四边形,∠EAD=∠BAF

(1)试说明:△CEF为等腰三角形;
(2)猜测CE与CF的和与□ABCD的周长有何关系,并说明理由.
【答案】(1)证明见解析;(2)CE与CF的和等于□ABCD的周长,理由见解析.
【解析】
(1)∵平行四边形的对边平行,∴AD∥BC,AB∥CD.又两直线平行,同位角相等,从而得∠E与∠F的关系,进而证明结论.
(2)□ABCD的周长=AB+BC+CD+DA.由(1)可证AD=DE,AB=BF.故CE+CF=□ABCD的周长.
解:(1)∵四边形ABCD是平行四边形.
∴AD∥BC,AB∥CD,∴∠EAD=∠F,∠BAF=∠E.
又∵∠EAD=∠BAF,∴∠E=∠F,∴CE=CF.
∴△CEF为等腰三角形.
(2)CE与CF的和等于□ABCD的周长.理由如下:
由(1)知∠E=∠BAF,
∵∠EAD=∠BAF.
∴∠E=∠EAD,∴AD=ED.
同理,AB=BF.
∴□ABCD的周长为AB+BC+DC+AD=BF+BC+CD+ED=CF+CE.
即CE与CF的和等于□ABCD的周长.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目