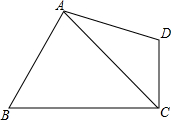
题目内容
如图,四边形ABCD中,CD=
,∠BCD=90°,∠B=60°,∠ACB=45°,∠CAD=30°,求AB的长.
| 2 |

过点D作DE⊥AC于E,过点A作AF⊥BC于F.
∵∠ACB=45°,∠BCD=90°,
∴∠ACD=45°.
∵CD=
,∴DE=EC=1.
∵∠CAD=30°,
∴AE=
=
.
∴AC=
+1.
∴FA=FC=
=
.
∵∠ABF=60°,
∴AB=
=
•
=
.

∵∠ACB=45°,∠BCD=90°,
∴∠ACD=45°.
∵CD=
| 2 |
∵∠CAD=30°,
∴AE=
| DE |
| tan30° |
| 3 |
∴AC=
| 3 |
∴FA=FC=
| ||
|
| ||||
| 2 |
∵∠ABF=60°,
∴AB=
| AF |
| sin60° |
| ||||
| 2 |
| 2 | ||
|
3
| ||||
| 3 |


练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目


 为60米,山坡AC的坡度i=1:1.(提示:坡面的铅直高度与水平宽度的比称为坡度)
为60米,山坡AC的坡度i=1:1.(提示:坡面的铅直高度与水平宽度的比称为坡度)

