题目内容
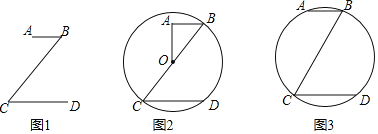
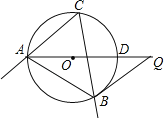
【题目】如图,⊙O是△ABC的外接圆,∠C=60°,AD是⊙O的直径,Q是AD延长线上的一点,且BQ=AB.
(1)求证:BQ是⊙O的切线;
(2)若AQ=6.
①求⊙O的半径;
②P是劣弧AB上的一个动点,过点P作EF∥AB,EF分别交CA、CB的延长线于E、F两点,连接OP,当OP和AB之间是什么位置关系时,线段EF取得最大值?判断并说明理由.
【答案】(1)详见解析;(2)①⊙O的半径为2;②当OP垂直平分AB时,线段EF取得最大值,理由详见解析.
【解析】
(1)根据同弧所对的圆周等于圆心角的一半,结合等腰三角形的性质,可求∠OBQ=90°;
(2)①设出半径,表示出OQ,运用三角函数建立方程即可求解;
②过点C作CH⊥EF,垂足为H,交AB于点K,推理出“EF随着HK的增大而增大,当HK取最大值时,EF取最大值”即可求解.
解:如图1,

(1)连接OB,
∵∠C=60°,
∴∠AOB=120°,
∵OA=OB,
∴∠OAB=∠OBA=30°,
∵BQ=AB,
∴∠Q=∠OAB=30°,
∴∠ABQ=120°,
∴∠OBQ=90°,
∴BQ是⊙O的切线;
(2)①设圆的半径为r,则OQ=6﹣r,
由(1)知,∠Q=30°,∠OBQ=90°,
∴![]() =sin30°=
=sin30°=![]() ,
,
∴![]() ,
,
解得:r=2;
②如图2,
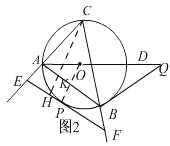
当OP垂直平分AB时,线段EF取得最大值;
理由如下:
由(1)知,AQ=6,∠Q=∠BAQ=30°,
可求AB=![]() ,
,
过点C作CH⊥EF,垂足为H,交AB于点K,
∵EF∥AB,
∴CK⊥AB,△ABC∽△EFC,
∴![]() ,
,
∴EF=![]() ,
,
易知:CK是定值,所以,EF随着HK的增大而增大,
当HK取最大值时,EF取最大值,
∴当点P为劣弧AB的中点时,HK最大,此时OP垂直平分AB.

 互动英语系列答案
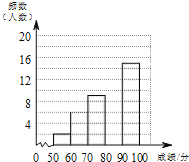
互动英语系列答案【题目】为了传承中华优秀传统文化,某校组织了一次八年级350名学生参加的“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分.为了更好地了解本次大赛的成绩分布情况,随机抽取了其中若干名学生的成绩作为样本进行整理,得到下列不完整的统计图表:
成绩x/分 | 频数 | 频率 |
50≤x<60 | 2 | 0.04 |
60≤x<70 | 6 | 0.12 |
70≤x<80 | 9 | b |
80≤x<90 | a | 0.36 |
90≤x≤100 | 15 | 0.30 |
请根据所给信息,解答下列问题:
(1)a= ,b= ;
(2)请补全频数分布直方图;
(3)这次比赛成绩的中位数会落在 分数段;
(4)若成绩在90分以上(包括90分)的为“优”等,则该年级参加这次比赛的350名学生中成绩“优”等的约有多少人?