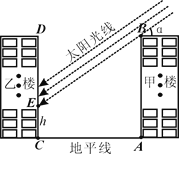
题目内容
【题目】点P为⊙O内一点,A、B、C、D为圆上顺次四个点,连接AB、CD,OM⊥AB于点M,连接MP并延长交CD于点N,连接PA、PB、PC、PD.
(1)如图1,若A、P、C三点共线,B、P、D三点共线,且AC⊥BD,求证:PN⊥CD;
(2)如图2,若PA=PD,PA⊥PD,PC=PB,PC⊥PB,求证:PN⊥CD;
(3)如图3,在(2)的条件下,PA=10,PC=6,∠APB=60°,求MN的长.
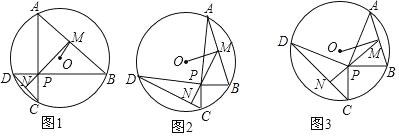
【答案】(1)见解析;(2)见解析;(3)7+![]()
【解析】
由OM⊥AB于点M,知M是AB的中点;
(1)∠APM+∠B=90°,证明∠APM=∠CPN即可;
(2)(3)通过作图证:△AEN≌△BPM(AAS)和△DPC≌△PAE(SAS)即可.
解:∵OM⊥AB于点M,
∴M是AB的中点;
(1)如图1,M是AB的中点,在Rt△APB中,∠A=∠APM,
∵AC⊥BD,
∴∠APB=90°,
∴∠A+∠B=90°,即:∠APM+∠B=90°,
而∠B=∠C,∠APM=∠CPN,即:∠CPN+∠C=90°,
∴PN⊥CD;
(2)如图:过A点作AE∥PB,延长PM至E,
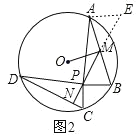
M是AB的中点,易证:△AEN≌△BPM(AAS),
∵AE∥PB,
∴∠EAP+∠APB=180°,
而∠DPC+∠APB=360°﹣90°﹣90°=180°,
∴∠EAP=∠DPC,
易证:△DPC≌△PAE(SAS),
∴∠APE=∠D,而∠APE+∠DPN=180°﹣90°=90°,
即:∠D+∠DPN=90°,
∴PN⊥CD;
(3)按照(2)的思路易证,
△AEN≌△BPM(AAS),△DPC≌△PAE(SAS),
∴PM=![]() PE,PE=CD,
PE,PE=CD,
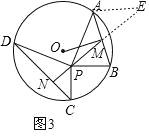
∵∠APB=60°,
∴∠DPC=360°﹣90°﹣90°﹣60°=120°,
在△DPC中,PD=PA=10,PC=6,∠DPC=120°,
易解,PN=![]() ,CD=14,
,CD=14,
而PM=![]() PE=
PE=![]() CD=7,
CD=7,
∴MN=PM+PN=7+![]() ,
,
即:MN的长为7+![]() .
.

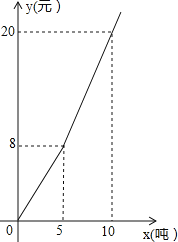
【题目】某水果店经销进价分别为![]() 元/千克、
元/千克、![]() 元/千克的甲、乙两种水果,下表是近两天的销售情况:(进价、售价均保持不变,利润=售价-进价)
元/千克的甲、乙两种水果,下表是近两天的销售情况:(进价、售价均保持不变,利润=售价-进价)
时间 | 甲水果销量 | 乙水果销量 | 销售收入 |
周五 |
|
|
|
周六 |
|
|
|
(1)求甲、乙两种水果的销售单价;
(2)若水果店准备用不多于![]() 元的资金再购进两种水果共
元的资金再购进两种水果共![]() 千克,求最多能够进甲水果多少千克?
千克,求最多能够进甲水果多少千克?
(3)在(2)的条件下,水果店销售完这![]() 千克水果能否实现利润为
千克水果能否实现利润为![]() 元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
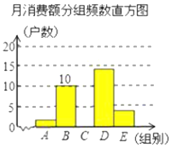
【题目】![]() 某校为了解七、八年级学生对“新冠”传播与防治知识的掌握情况,从七、八年级各随机抽取50名学生进行测试,并对成绩(百分制)进行整理和分析.部分信息如下:
某校为了解七、八年级学生对“新冠”传播与防治知识的掌握情况,从七、八年级各随机抽取50名学生进行测试,并对成绩(百分制)进行整理和分析.部分信息如下:
a.七年级成绩频数分布直方图:
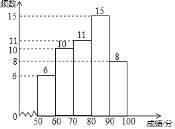
b.七年级成绩在70![]() m
m![]() 80这一组的是:
80这一组的是:
70,72,72,75,76,76,77,77,78,79,79
c.七、八年级成绩的平均数、中位数如下:
年级 | 平均数 | 中位数 |
七 | 76.9 | a |
八 | 79.2 | 79.5 |
根据以上信息,回答下列问题:
(1)在这次测试中,七年级在70分以上的有 人,表格中a的值为 ;
(2)在这次测试中,七年级学生甲与八年级学生乙的成绩都是79分,请判断两位学生在各自年级的排名谁更靠前;
(3)该校七年级学生有500人,假设全部参加此次测试,请你估计七年级成绩超过平均数76.9分的人数.