题目内容
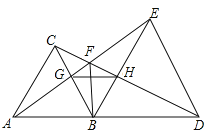
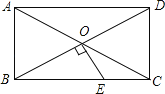
【题目】在长方形ABCD内,将两张边长分别为a和b(a>b)的正方形纸片按图1,图2两种方式放置(图1,图2中两张正方形纸片均有部分重叠),设图1中未被这两张正方形纸片覆盖的面积为S1,图2中未被这两张正方形纸片覆盖的面积为S2,当S2-S1=b时,AD-AB的值为( )

A.1B.2C.2a-2bD.b
【答案】A
【解析】
根据图1、图2的放置方式,分别用含AB、AD、a、b的代数式表示出S1、S2,进而可得S1-S2,根据S2-S1=b即可得答案.
∵矩形ABCD,
∴AD=BC,AB=CD
由图1和图2可知
S1=a(AB-a)+(AB-b)(AD-a)=AB·AD-a2-AD·b+ab;
S2=AB(AD-a)+(AB-a)(a-b)=AB·AD-a2-AB·b+ab;
∴S2-S1=(AB·AD-a2-AB·b+ab)-(AB·AD-a2-AB·b+ab)
=(AD-AB)·b;
∵S2-S1=b,
∴(AD-AB)·b=b
∴b(AD-AB-1)=0,
∵b≠0
∴AD-AB-1=0
解得:AD-AB=1
故选A.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
【题目】“保护环境,人人有责”,为了更好的治理好金水河,郑州市污水处理厂决定购买![]() 、
、![]() 两型号污水处理设备共10台,其信息如下表:
两型号污水处理设备共10台,其信息如下表:
单价(万元/台) | 每台处理污水量(吨/月) | |
| 12 | 220 |
| 10 | 200 |
(1)设购买![]() 设备
设备![]() 台,所需资金共为W万元,每月处理污水总量为y吨,试写出W与
台,所需资金共为W万元,每月处理污水总量为y吨,试写出W与![]() ,
,![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)经预算,市污水处理厂购买设备的资金不超过106万元,月处理污水量不低于2040吨,请你列举出所有购买方案,并指出哪种方案更省钱,需要多少资金?