��Ŀ����
����Ŀ����������ABCD�У�����BD��
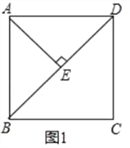
��1����ͼ1��AE��BD��E��ֱ��д����BAE�Ķ�����
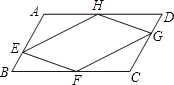
��2����ͼ1���ڣ�1���������£�����AEB��A��ת���ģ�����ʱ�뷽����ת30���õ���AB��E�䣬AB����BD����M��AE����ӳ�����BD����N��
�������ⲹȫͼ1��
���õ�ʽ��ʾ�߶�BM��DN��MN֮���������ϵ����֤����
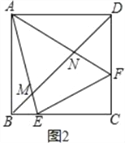
��3����ͼ2��E��F�DZ�BC��CD�ϵĵ㣬��CEF�ܳ���������ABCD�ܳ���һ�룬AE��AF�ֱ���BD����M��N��д���ж��߶�BM��DN��MN֮��������ϵ��˼·��������д�������������̣�
���𰸡���1����BAE�Ķ���Ϊ45�㣻��2���ٲ�ȫͼ����������BM��DN��MN֮���������ϵ��BM2+MD2=MN2�����ɼ���������3��˼·������.
����������1�����õ���ֱ�������ε����ʼ��ɣ�
��2�������⻭����ͼ1��ʾ��ͼ�Σ��������ʺ������ε����ʣ��ж��߶εĹ�ϵ�������ù��ɶ����õ�FB2+BM2=FM2�����жϳ�FM=MN���ɣ�
��3�����á�CEF�ܳ���������ABCD�ܳ���һ�룬�жϳ�EF=EG�������ã�2��֤�����ɣ�
�⣺��1����BD��������ABCD�ĶԽ��ߣ����ABD=��ADB=45�㣬
��AE��BD�����ABE=��BAE=45�㣬
��2���������ⲹȫͼ�Σ���ͼ1��ʾ��

��BM��DN��MN֮���������ϵ��BM2+MD2=MN2��
����AND�Ƶ�D˳ʱ����ת90�㣬�õ���AFB��
���ADB=��FBA����BAF=��DAN��DN=BF��AF=AN��
����������ABCD�У�AE��BD�����ADB=��ABD=45�㣬
���FBM=��FBA+��ABD=��ADB+��ABD=90�㣬
��Rt��BFM�У����ݹ��ɶ����ã�FB2+BM2=FM2��
����ת��ANE�õ�AB1E1�����E1AB1=45�㣬���BAB1+��DAN=90�㩁45��=45�㣬
�ߡ�BAF=DAN�����BAB1+��BAF=45�㣬���FAM=45�㣬���FAM=��E1AB1��
��AM=AM��AF=AN�����AFM�ա�ANM����FM=MN��
��FB2+BM2=FM2����DN2+BM2=MN2��
��3����ͼ2��

����ADF�Ƶ�A˳ʱ����ת90��õ���ABG����DF=GB��
��������ABCD���ܳ�Ϊ4AB����CEF�ܳ�ΪEF+EC+CF��
�ߡ�CEF�ܳ���������ABCD�ܳ���һ�룬��4AB=2��EF+EC+CF������2AB=EF+EC+CF
��EC=AB��BE��CF=AB��DF����2AB=EF+AB��BE+AB��DF����EF=DF+BE��
��DF=GB����EF=GB+BE=GE������ת�õ�AD=AG=AB��
��AM=AM�����AEG�ա�AEF����EAG=��EAF=45�㣬�ͣ�2���Ģ�һ�����õ�DN2+BM2=MN2��
���㾦���������ı����ۺ��⣬��Ҫ�����������ε����ʡ���ת�����ʣ������ε�ȫ�ȣ��жϳ�����AFN�ա�ANM���õ�FM=MM�����ǽ���Ĺؼ�.

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�