��Ŀ����
����Ŀ���ٶ��̲ģ����볤�ı���![]() ��ԼΪ
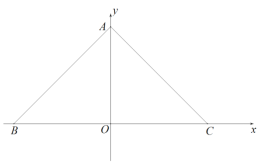
��ԼΪ![]() ���ľ��ν����ƽ���Σ��ƽ���θ�������Э�����ȳƵ����У�����������������Ľ�����Ϊȡ����ѵ��Ӿ�Ч�����������˻ƽ���ε���ƣ����������ÿ�Ϊ
���ľ��ν����ƽ���Σ��ƽ���θ�������Э�����ȳƵ����У�����������������Ľ�����Ϊȡ����ѵ��Ӿ�Ч�����������˻ƽ���ε���ƣ����������ÿ�Ϊ![]() �ľ���ֽƬ�۵��ƽ���Σ���ʾ��
�ľ���ֽƬ�۵��ƽ���Σ���ʾ��![]() ��
��
��һ�����ھ���ֽƬһ������ͼ�ٵķ����۳�һ�������Σ�Ȼ���ֽƬչƽ��

�ڶ�������ͼ����������������۳�������ȵľ��Σ��ٰ�ֽƬչƽ��

���������۳��ڲ���εĶԽ���![]() ������
������![]() �۵�ͼ������ʾ��
�۵�ͼ������ʾ��![]() ����
����

���IJ���չƽֽƬ���������õĵ�![]() �۳�
�۳�![]() ʹ
ʹ![]() ��ͼ���оͻ���ֻƽ���Σ�
��ͼ���оͻ���ֻƽ���Σ�

��������
��1��ͼ����![]() _ ���������ţ���
_ ���������ţ���
��2����ͼ�����ж��ı���![]() ����״����˵�����ɣ�
����״����˵�����ɣ�
��3����д��ͼ�������еĻƽ���Σ���ѡ������һ��˵�����ɣ�
���𰸡���1��![]() ����2�����Σ�����������3���ƽ�����о���
����2�����Σ�����������3���ƽ�����о���![]() ������
������![]() ��������
��������
��������
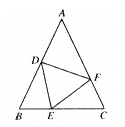
��1���������֪��NC=BC=2����BCN=90�㣬��AΪNC���е㣬�Ӷ����AC��Ȼ�����ù��ɶ�������������ۣ�
��2�����ݾ��ε����ʺ�ƽ���ߵ����ʿɵ�![]() ,Ȼ������۵������ʿɵ�
,Ȼ������۵������ʿɵ�![]() ���Ӷ�֤��
���Ӷ�֤��![]() ������֤���ı���
������֤���ı���![]() ��ƽ���ı��Σ��ٸ������ε��ж���������֤�����ۣ�
��ƽ���ı��Σ��ٸ������ε��ж���������֤�����ۣ�
��3�����ݻƽ���μ���֤�����ۣ�
�⣺![]() �������֪��NC=BC=2����BCN=90�㣬��AΪNC���е�
�������֪��NC=BC=2����BCN=90�㣬��AΪNC���е�
��AC= ![]() NC=1
NC=1
��AB=![]() =
=![]()
�ʴ�Ϊ��![]() ��
��
![]() �ı���
�ı���![]() ������
������
![]() ��ͼ
��ͼ![]() ���ı���
���ı���![]() �Ǿ��Σ�
�Ǿ��Σ�
![]()
![]()
���۵��ã�![]()
![]()
![]()
![]()
![]()
![]() �ı���
�ı���![]() ��ƽ���ı���
��ƽ���ı���
![]()
![]() �ı���
�ı���![]() ������
������
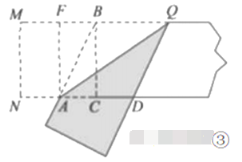
![]() ��ͼ�еĻƽ�����о���
��ͼ�еĻƽ�����о���![]() ������
������![]()
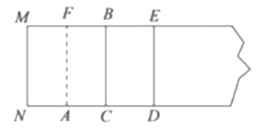
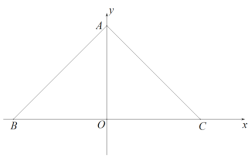
�Ծ���![]() Ϊ������������:
������������:
![]() ��
��
![]() ��
��
��![]()
![]()
![]() ����
����![]() �ǻƽ���Σ�
�ǻƽ���Σ�
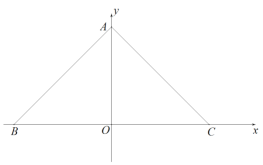
�Ծ���![]() Ϊ������������:
������������:
![]() ��AM=2
��AM=2
![]() ��
��
![]()
![]() ����
����![]() �ǻƽ���Σ�
�ǻƽ���Σ�

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�