题目内容
【题目】某商场用24000元购入一批空调,然后以每台3000元的价格销售,因天气炎热,空调很快售完;商场又以52000元的价格再次购入该种型号的空调,数量是第一次购入的2倍,但购入的单价上调了200元,售价每台也上调了200元.
(1)商场第一次购入的空调每台进价是多少元?
(2)商场既要尽快售完第二次购入的空调,又要在这两次空调销售中获得的利润率不低于22%,打算将第二次购入的部分空调按每台九五折出售,最多可将多少台空调打折出售?
【答案】(1)2400元;(2)8台.
【解析】试题分析:(1)设商场第一次购入的空调每台进价是x元,根据题目条件“商场又以52000元的价格再次购入该种型号的空调,数量是第一次购入的2倍,但购入的单价上调了200元,每台的售价也上调了200元”列出分式方程解答即可;
(2)设最多将![]() 台空调打折出售,根据题目条件“在这两次空调销售中获得的利润率不低于22%,打算将第二次购入的部分空调按每台九五折出售”列出不等式并解答即可.
台空调打折出售,根据题目条件“在这两次空调销售中获得的利润率不低于22%,打算将第二次购入的部分空调按每台九五折出售”列出不等式并解答即可.
试题解析:(1)设第一次购入的空调每台进价是x元,依题意,得
![]() 解得
解得![]()
经检验, ![]() 是原方程的解.
是原方程的解.
答:第一次购入的空调每台进价是2 400元.
(2)由(1)知第一次购入空调的台数为24 000÷2 400=10(台),第二次购入空调的台数为10×2=20(台).
设第二次将y台空调打折出售,由题意,得
![]() 解得
解得![]()
答:最多可将8台空调打折出售.
【题型】解答题
【结束】
23
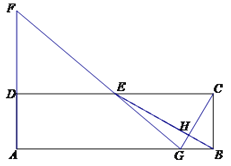
【题目】在矩形ABCD中,E为CD的中点,H为BE上的一点,,连接CH并延长交AB于点G,连接GE并延长交AD的延长线于点F.
(1)求证: AB·BH=2BG·EH
(2)若∠CGF=90°,![]() =3时,求
=3时,求![]() 的值.
的值.
【答案】(1)见解析;(2)![]()
【解析】分析(1)根据相似三角形判定的方法,判断出△CEH∽△GBH,即可证明![]() .再由EC=
.再由EC=![]() CD=
CD=![]() AB可得结论;
AB可得结论;
(2)作EM⊥AB于M,则EM=BC=AD,AM=DE,设DE=CE=3a,则AB=CD=6a,由(1)得:![]() =3,得出BG=
=3,得出BG=![]() CE=a,AG=5a,证明△DEF∽△GEC,由相似三角形的性质得出EGEF=DEEC,由平行线证出
CE=a,AG=5a,证明△DEF∽△GEC,由相似三角形的性质得出EGEF=DEEC,由平行线证出![]() ,得出EF=
,得出EF= ![]() EG,求出EG=
EG,求出EG=![]() a,在Rt△EMG中,GM=2a,由勾股定理求出BC=EM=
a,在Rt△EMG中,GM=2a,由勾股定理求出BC=EM=![]() a,即可得出结果.
a,即可得出结果.
详解:(1)证明:∵四边形ABCD是矩形,
∴CD∥AB,
∴∠ECH=∠BGH,∠CEH=∠GBH,
∴△CEH∽△GBH,
∴![]() .
.
∴EC·BH=BG·EH
∴![]() AB·BH=BG·EH
AB·BH=BG·EH
∴AB·BH=2BG·EH
(2)作EM⊥AB于M,如图所示:
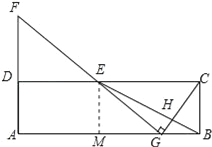
则EM=BC=AD,AM=DE,
∵E为CD的中点,
∴DE=CE,
设DE=CE=3a,则AB=CD=6a,
由(1)得:![]() =3,
=3,
∴BG=![]() CE=a,
CE=a,
∴AG=5a,
∵∠EDF=90°=∠CGF,∠DEF=∠GEC,
∴△DEF∽△GEC,
∴![]() ,
,
∴EGEF=DEEC,
∵CD∥AB,
∴![]() ,
,
∴![]() ,
,
∴EF=![]() EG,
EG,
∴EG![]() EG=3a3a,
EG=3a3a,
解得:EG=![]() a,
a,
在Rt△EMG中,GM=2a
∴EM=![]() a,
a,
∴BC=![]() a,
a,
∴![]() =
=![]()