题目内容
如图，⊙O的直径AB垂直于弦CD，垂足为H．点P是弧AC上一点（点P不与A、C两点重合）．连接PC、PD、PA、AD，点E在AP的延长线上，PD与AB交于点F．给出下列四个结论：①CH2=AH•BH；②
；③AD2=DF•DP；④∠EPC=∠APD．其中正确的结论是________．（只填序号）
①②④
分析：根据圆周角定理，垂径定理，圆内接四边形的性质，相交弦定理，对4个结论逐一分析即可．
解答：
证明：①由相交弦定理知，CH•HD=CH2=AH•BH，
故①正确；
②∵H是CD的中点，
∴
=
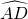，（垂径定理）
故②正确；
③连接BD，
∵直径AB垂直于弦CD，垂足为H，
∴△ADH∽△ADB，
∴可得AD2=AH•AB，
故③不正确，
④∵弧AC对的圆周角为∠ADC，弧AD对的圆周角为∠APD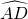，=，②已证
∴∠ADC=∠APD，
∵∠EPC=∠ADC，由圆内接四边形的外角等于它的内对角知
∴∠EPC=∠APD，
故④正确．综上所述，正确的有①②④．
故答案为：①②④．
点评：本题考查了相似三角形的判定与性质，圆周角定理，垂径定理，圆内接四边形的性质等知识点，综合性较强．难易程度适中，是一道很典型的题目．
分析：根据圆周角定理，垂径定理，圆内接四边形的性质，相交弦定理，对4个结论逐一分析即可．
解答：
证明：①由相交弦定理知，CH•HD=CH2=AH•BH，故①正确；
②∵H是CD的中点，
∴
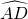=，（垂径定理）故②正确；
③连接BD，
∵直径AB垂直于弦CD，垂足为H，
∴△ADH∽△ADB，
∴可得AD2=AH•AB，
故③不正确，
④∵弧AC对的圆周角为∠ADC，弧AD对的圆周角为∠APD，
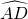=，②已证∴∠ADC=∠APD，
∵∠EPC=∠ADC，由圆内接四边形的外角等于它的内对角知
∴∠EPC=∠APD，
故④正确．综上所述，正确的有①②④．
故答案为：①②④．
点评：本题考查了相似三角形的判定与性质，圆周角定理，垂径定理，圆内接四边形的性质等知识点，综合性较强．难易程度适中，是一道很典型的题目．
练习册系列答案
相关题目
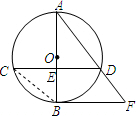已知：如图，⊙O的直径AB与弦CD相交于E，
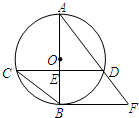如图，⊙O的直径AB与弦CD（不是直径）相交于E，E是CD的中点，过点B作BF∥CD交AD的延长线于
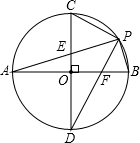如图，⊙O的直径AB，CD互相垂直，P为 上任意一点，连PC，PA，PD，PB，下列结论：
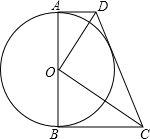（2013•柳州）如图，⊙O的直径AB=6，AD、BC是⊙O的两条切线，AD=2，BC=
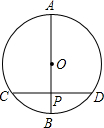如图，⊙O的直径AB垂直弦CD于P，且P是半径OB的中点，CD=6cm，则直径AB的长是