题目内容
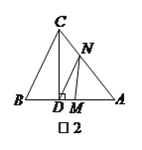
【题目】如图,在△ABC中,∠C=90°,∠B=30°,AD是△ABC的角平分线,DE∥BA交AC于点E,DF∥CA交AB于点F,已知CD=3. 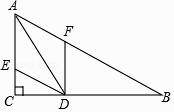
(1)求AD的长;
(2)求四边形AEDF的周长.(注意:本题中的计算过程和结果均保留根号)
【答案】
(1)解:∵∠C=90°,∠B=30°,
∴∠CAB=60°,
∵AD平分∠CAB,
∴∠CAD= ![]() ∠CAB=30°,
∠CAB=30°,
在Rt△ACD中,∵∠ACD=90°,∠CAD=30°,
∴AD=2CD=6.
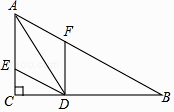
(2)解:∵DE∥BA交AC于点E,DF∥CA交AB于点F,
∴四边形AEDF是平行四边形,
∵∠EAD=∠ADF=∠DAF,
∴AF=DF,
∴四边形AEDF是菱形,
∴AE=DE=DF=AF,
在Rt△CED中,∵∠CDE=∠B=30°,
∴DE= ![]() =2
=2 ![]() ,
,
∴四边形AEDF的周长为8 ![]() .
.
【解析】(1)首先证明∠CAD=30°,易知AD=2CD即可解决问题;(2)首先证明四边形AEDF是菱形,求出ED即可解决问题;
【考点精析】本题主要考查了平行线的性质和含30度角的直角三角形的相关知识点,需要掌握两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补;在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半才能正确解答此题.

练习册系列答案
相关题目