题目内容
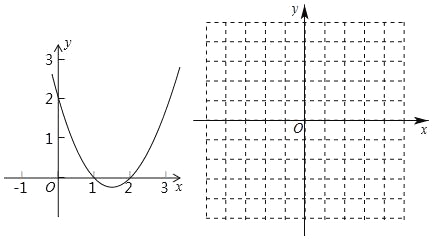
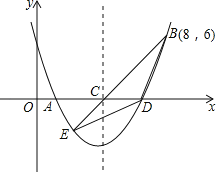
【题目】如图,二次函数y=![]() x2+bx+c的图象交x轴于A、D两点,并经过B点,已知A点坐标是(2,0),B点的坐标是(8,6).
x2+bx+c的图象交x轴于A、D两点,并经过B点,已知A点坐标是(2,0),B点的坐标是(8,6).
(1)求二次函数的解析式.
(2)求函数图象的顶点坐标及D点的坐标.
(3)该二次函数的对称轴交x轴于C点.连接BC,并延长BC交抛物线于E点,连接BD,DE,求△BDE的面积.
(4)抛物线上有一个动点P,与A,D两点构成△ADP,是否存在S△ADP=![]() S△BCD?若存在,请求出P点的坐标;若不存在.请说明理由.
S△BCD?若存在,请求出P点的坐标;若不存在.请说明理由.
【答案】(1)二次函数解析式为:y=![]() x2﹣4x+6;
x2﹣4x+6;
(2)函数图象的顶点坐标为(4,﹣2),点D的坐标为(6,0);
(3)△BDE的面积为7.5.
(4)存在,P1(4+![]() ,
,![]() ),P2(4﹣
),P2(4﹣![]() ,
,![]() ),P3(3,﹣
),P3(3,﹣![]() ),P4(5,﹣
),P4(5,﹣![]() ).
).
【解析】
试题(1)利用待定系数法求出b,c即可求出二次函数解析式;
(2)把二次函数式转化可直接求出顶点坐标,由A对称关系可求出点D的坐标;
(3)由待定系数法可求出BC所在的直线解析式,与抛物线组成方程求出点E的坐标,利用△BDE的面积=△CDB的面积+△CDE的面积求出△BDE的面积;
(4)设点P到x轴的距离为h,由S△ADP=![]() S△BCD求出h的值,根据h的正,负值求出点P的横坐标即可求出点P的坐标.
S△BCD求出h的值,根据h的正,负值求出点P的横坐标即可求出点P的坐标.
试题解析:(1)∵二次函数y=![]() x2+bx+c的图象过A(2,0),B(8,6)
x2+bx+c的图象过A(2,0),B(8,6)
∴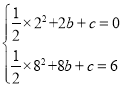 ,解得
,解得![]()
∴二次函数解析式为:y=![]() x2﹣4x+6;
x2﹣4x+6;
(2)由y=![]() x2﹣4x+6,得y=
x2﹣4x+6,得y=![]() (x﹣4)2﹣2,
(x﹣4)2﹣2,
∴函数图象的顶点坐标为(4,﹣2),
∵点A,D是y=![]() x2+bx+c与x轴的两个交点,
x2+bx+c与x轴的两个交点,
又∵点A(2,0),对称轴为x=4,
∴点D的坐标为(6,0);
(3)∵二次函数的对称轴交x轴于C点.
∴C点的坐标为(4,0)
∵B(8,6),
设BC所在的直线解析式为y=kx+b,
∴![]() 解得
解得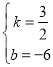
∴BC所在的直线解析式为y=![]() x﹣6,
x﹣6,
∵E点是y=![]() x﹣6与y=
x﹣6与y=![]() x2﹣4x+6的交点,
x2﹣4x+6的交点,
∴![]() x﹣6=
x﹣6=![]() x2﹣4x+6
x2﹣4x+6
解得x1=3,x2=8(舍去),
当x=3时,y=﹣3,
∴E(3,﹣![]() ),
),
∴△BDE的面积=△CDB的面积+△CDE的面积=![]() ×2×6+
×2×6+![]() ×2×
×2×![]() =7.5.
=7.5.
(4)存在,
设点P到x轴的距离为h,
∵S△BCD=![]() ×2×6=6,S△ADP=
×2×6=6,S△ADP=![]() ×4×h=2h,
×4×h=2h,
∵S△ADP=![]() S△BCD
S△BCD
∴2h=6×![]() ,解得h=
,解得h=![]() ,
,
当P在x轴上方时,
![]() =
=![]() x2﹣4x+6,解得x1=4+
x2﹣4x+6,解得x1=4+![]() ,x2=4﹣
,x2=4﹣![]() ,
,
当当P在x轴下方时,
﹣![]() =
=![]() x2﹣4x+6,解得x1=3,x2=5,
x2﹣4x+6,解得x1=3,x2=5,
∴P1(4+![]() ,
,![]() ),P2(4﹣
),P2(4﹣![]() ,
,![]() ),P3(3,﹣
),P3(3,﹣![]() ),P4(5,﹣
),P4(5,﹣![]() ).
).

【题目】甲、乙两名队员参加设计训练,成绩分别被制成下列两个统计图:
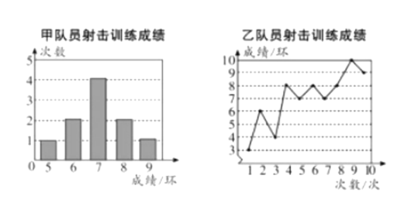
根据以上信息,整理分析数据如下:
平均数(环) | 中位数(环) | 众数(环) | 方差 | |
甲 |
|
|
|
|
乙 |
|
|
|
|
(1)表格中![]() ,
,![]() ,
,![]() ;
;
(2)分别运用表中的四个统计量,简要分析这两名队员的射击训练成绩,若选派其中一名参赛,你认为应选哪名队员?
(3)如果乙再射击![]() 次,命中
次,命中![]() 环,那么乙的射击成绩的方差 .(填“变大”“变小”或“不变”)
环,那么乙的射击成绩的方差 .(填“变大”“变小”或“不变”)