Question

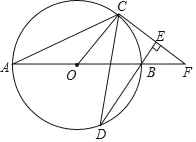
【题目】如图，AB为⊙O直径，C、D为⊙O上不同于A、B的两点，OC平分∠ACD，过点C作CE⊥DB，垂足为E，直线AB与直线CE相交于F点．

（1）求证：CF为⊙O的切线；

（2）当BF=2，∠F=30°时，求BD的长．

Answer 1

【答案】（1）见解析；（2）2.

【解析】

（1）根据角平分线的定义和根据切线的判定即可证明CF为⊙O的切线；

（2）连结AD．根据相似三角形的判定和性质解答即可．

（1）∵OC平分∠ACD，

∴∠ACO=∠OCD，

∵∠A=∠D=∠ACO，

∴∠D=∠OCD，

∴OC∥DE，

∵DE⊥CF，

∴OC⊥CF，

∴CF为⊙O的切线；

（2）连接AD，

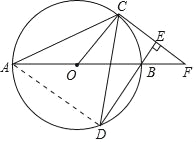
∵BE∥OC，

∴△FEB∽△FCO，

∴= ，

解得：r=2，

∴AB=4，

∵∠ABD=60°，

∴BD=2．