题目内容
【题目】(1)观察发现:如图1,已知Rt△ABC,∠ABC=90°,分别以AB,BC为边,向外作正方形ABDE和正方形BCFG,连接DG.若M是DG的中点,不难发现:BM=![]() AC.
AC.
请完善下面证明思路:①先根据 ,证明BM=![]() DG;②再证明 ,得到DG=AC;所以BM=
DG;②再证明 ,得到DG=AC;所以BM=![]() AC;
AC;
(2)数学思考:若将上题的条件改为:“已知Rt△ABC,∠ABC=90°,分别以AB,AC为边向外作正方形ABDE和正方形ACHI,N是EI的中点”,则相应的结论“AN=![]() BC”成立吗?
BC”成立吗?
小颖通过添加如图2所示的辅助线验证了结论的正确性.请写出小颖所添加的辅助线的作法,并由此证明该结论;
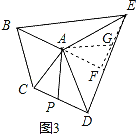
(3)拓展延伸:如图3,已知等腰△ABC和等腰△ADE,AB=AC,AD=AE.连接BE,CD,若P是CD的中点,探索:当∠BAC与∠DAE满足什么条件时,AP=![]() BE,并简要说明证明思路.
BE,并简要说明证明思路.

【答案】(1)直角三角形斜边上的中线等于斜边的一半,△BDG≌△BAC;(2)能,理由见解析;(3)当∠BAC=∠DAE=90°时,AP=![]() BE,
BE,
【解析】试题分析:(1)根据题意即可得到结论;
(2)过I作IK⊥EA交EA的延长线于K,根据平角的定义得到∠BAC=∠IAK,根据全等三角形的性质得到BC=IK,AB=AK,等量代换得到AE=AI,推出AN是△EKI的中位线,于是得到结论.
(3)延长BA到F,使AF=AB,连接EF,过A作AG∥BE,根据三角形中位线的性质得到AG=![]() BE,根据全等三角形的性质得到∠ADC=∠AEF,EF=CD,根据全等三角形的性质即可得到结论.
BE,根据全等三角形的性质得到∠ADC=∠AEF,EF=CD,根据全等三角形的性质即可得到结论.
试题解析:
(1)①直角三角形斜边上的中线等于斜边的一半,②△BDG≌△BAC;
故答案为:直角三角形斜边上的中线等于斜边的一半,△BDG≌△BAC;
(2)能,
理由:过I作IK⊥EA交EA的延长线于K,
∵∠EAI+∠BAC=360°﹣90°﹣90°=180°,∠EAI+∠TAK=180°,
∵∠BAC=∠IAK,
在△ABC与△AKI中, ,
,
∴△ABC≌△AKI,
∴BC=IK,AB=AK,
∵AE=AB,
∴AE=AI,
∵N是EI的中点,
∴AN是△EKI的中位线,
∴AN=![]() IK,
IK,
∴AN=![]() BC;
BC;
(3)当∠BAC=∠DAE=90°时,AP=![]() BE,
BE,
延长BA到F,使AF=AB,连接EF,过A作AG∥BE,
∴EG=![]() EF,
EF,
∴AG=![]() BE,
BE,
∵∠BAC=∠DAE=90°,
∴∠CAD=180°﹣∠BAE,
∵∠FAE=180°﹣BAE,
∴∠CAD=∠FAE,
在△ACD与△AFE中, ,
,
∴△ACD≌△FAE,
∴∠ADC=∠AEF,EF=CD,
∵P是CD的中点,
∴DP=![]() CD,
CD,
∴EG=DP,
在△ADP与△AEG中,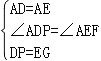 ,
,
∴△ADP≌△AEG,
∴AP=AG,
∴AP=![]() BE.
BE.