题目内容

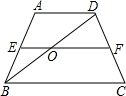
已知：如图，梯形ABCD中，AD∥BC，AB=DC，AD=2cm，中位线长5cm，高AE=33cm．求这个梯形的腰长．
由中位线定理，得中位线长=
2+BC
2
=5，
∴BC=8，（2分）
∴四边形ABCD是等腰梯形，
∴BE=
BC-AD
2
=
8-2
2
=3，
在Rt△AEB中，AB=
AE2+BE2
=6（cm）．（5分）
练习册系列答案
相关题目
菱形周长是20，对角线长的比为3：4，则菱形的面积为______．
如图，已知等腰梯形ABCD的底角∠B=45°，高AE=1，上底AD=1，则其面积为（　　）
A．4B．2
2
C．1D．2
等腰梯形的一个底角为45°，高为h，那么两底之差等于______．
如图，梯形ABCD中，AD∥BC，BD为对角线，中位线EF交BD于O点，若FO-EO=3，则BC-AD等于（　　）
A．4B．6C．8D．10
如图，在等腰梯形ABCD中，AB∥DC，AB=8cm，CD=2cm，AD=6cm．点P从点A出发，以2cm/s的速度沿AB向终点B运动；点Q从点C出发，以1cm/s的速度沿CD、DA向终点A运动（P、Q两点中，有一个点运动到终点时，所有运动即终止）．设P、Q同时出发并运动了t秒．
（1）当PQ将梯形ABCD分成两个直角梯形时，求t的值；
（2）试问是否存在这样的t，使四边形PBCQ的面积是梯形ABCD面积的一半？若存在，求出这样的t的值；若不存在，请说明理由．
如图，已知EF是梯形ABCD的中位线，△DEF的面积为5cm2，则梯形ABCD的面积为______cm2．
若等腰梯形的两条对角线互相垂直，中位线长为8cm，则该等腰梯形的面积为（　　）cm2．
A．16B．32C．64D．512
如图，等腰梯形ABCD中，AD∥BC，∠B=60°，则∠D=______度．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网