题目内容
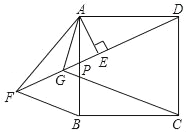
【题目】如图，已知抛物线
与直线y=2x+3交于点M（0，3）， A（a，15）．点B是抛物线上M，A之间的一个动点，过点B分别作x轴、y轴的平行线与直线MA交于点C，E．以BC，BE为边构造矩形BCDE，设点D的坐标为（m，n），请写出m，n之间的关系式________________ ．
【答案】
【解析】试题解析：∵点A（a，15）在直线y=2x+3上，
∴12=2a，
解得：a=6，
又∵点A、M是抛物线y=
x2+bx+c上的点，
将点A（6，15）、M（0，3）代入y=
x2+bx+c，可得
，解得： 
∴抛物线解析式为y=
x2-x+3．
∵直线MA的解析式为：y=2x+3，点D的坐标为（m，n），
∴点E的坐标为（
，n），点C的坐标为（m，2m+3），
∴点B的坐标为（
，2m+3），
把点B（
，2m+3）代入y=
x2-x+3，可得m=
∴m、n之间的关系式为m=
.
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
【题目】为了解上一次八年级数学测验成绩情况，随机抽取了40名学生的成绩进行统计分析，这40名学生的成绩数据如下：
55 62 67 53 58 83 87 64 68 85
60 94 81 98 51 83 78 77 66 71
91 72 63 75 88 73 52 71 79 63
74 67 78 61 97 76 72 77 79 71
（1）将样本数据适当分组，制作频数分布表：
分 组 |
|
|
|
|
|
频 数 |
|
|
|
|
|
（2）根据频数分布表，绘制频数直方图：
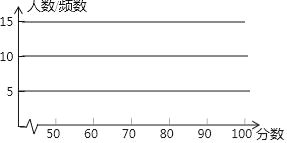
（3）从图可以看出，这40名学生的成绩都分布在什么范围内？分数在哪个范围的人数最多？
