题目内容
已知等腰三角形△ABC中,AB=AC,∠C的平分线与AB边交于点P,M为△ABC的内切圆⊙I与BC边的切点,作MD∥AC,交⊙I于点D.
证明:PD是⊙I的切线.
证明:PD是⊙I的切线.
分析:过P点作出圆的切线,Q点为切点,通过证明Q点与D点重合来证明DPD与圆相切.
解答: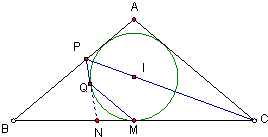 证明:过点P作⊙I的切线PQ(切点为Q)并延长,交BC于点N.
证明:过点P作⊙I的切线PQ(切点为Q)并延长,交BC于点N.
∵CP为∠ACB的平分线,
∴∠ACP=∠BCP.
又∵PA、PQ均为⊙I的切线,
∴∠APC=∠NPC.
又CP公共边,
∴△ACP≌△NCP,
∴∠PAC=∠PNC.
由NM=QN,BA=BC,
∴△QNM∽△BAC,
故∠NMQ=∠ACB,
∴MQ∥AC
又∵MD∥AC,
∴MD和MQ为同一条直线.
又点Q、D均在⊙I上,
∴点Q和点D重合,
故PD是⊙I的切线.
 证明:过点P作⊙I的切线PQ(切点为Q)并延长,交BC于点N.
证明:过点P作⊙I的切线PQ(切点为Q)并延长,交BC于点N.∵CP为∠ACB的平分线,
∴∠ACP=∠BCP.
又∵PA、PQ均为⊙I的切线,
∴∠APC=∠NPC.
又CP公共边,
∴△ACP≌△NCP,
∴∠PAC=∠PNC.
由NM=QN,BA=BC,
∴△QNM∽△BAC,
故∠NMQ=∠ACB,
∴MQ∥AC
又∵MD∥AC,
∴MD和MQ为同一条直线.
又点Q、D均在⊙I上,
∴点Q和点D重合,
故PD是⊙I的切线.
点评:本题考查了切线的证明,和以往证明切线不同,本题采用了一种全新的证明切线的方法,即:作圆的切线,证明要证明的切线与所作切线重合.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
已知等腰三角形ABC中,AB=AC=
,底角为30°,动点P从点B向点C运动,当运动到PA与一腰垂直时BP长为( )
| 3 |
| A、1 | ||
| B、1或3 | ||
| C、1或2 | ||
D、
|
 如图,已知等腰三角形ABC中,底边BC=24cm,△ABC的面积等于60cm2.
如图,已知等腰三角形ABC中,底边BC=24cm,△ABC的面积等于60cm2.