题目内容
已知等腰三角形ABC中，AB=AC=
，底角为30°，动点P从点B向点C运动，当运动到PA与一腰垂直时BP长为（ ）
| 3 |
| A、1 | ||
| B、1或3 | ||
| C、1或2 | ||
D、
|
分析：根据题意可分两种情况讨论：①PA⊥AC；②PA⊥AB；可求得BP值．
解答：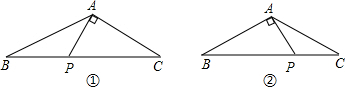
解：①如图当PA⊥AC时；
∵AB=AC，∴∠B=∠C=30°，
∴∠APC=60°，∠BAP=30°，
∴PA=PB，
∵AC=
，∴AP=1，
∴PB=1；
②当PA⊥AB时；
∵AB=AC，∴∠B=∠C=30°，
∴∠APB=60°，∠CAP=30°，
∴PA=PC，
∵AC=
，∴AP=1，BP=2．
故选C．
解：①如图当PA⊥AC时；∵AB=AC，∴∠B=∠C=30°，
∴∠APC=60°，∠BAP=30°，
∴PA=PB，
∵AC=
| 3 |
∴PB=1；
②当PA⊥AB时；
∵AB=AC，∴∠B=∠C=30°，
∴∠APB=60°，∠CAP=30°，
∴PA=PC，
∵AC=
| 3 |
故选C．
点评：本题考查了等腰三角形的性质，解直角三角形的有关知识，注意分类讨论思想的应用．
练习册系列答案
相关题目
15、如图，已知等腰三角形ABC中，AC=BC，D为BC边上一点，且AB=AD，若不再添加辅助线，图中与∠C相等的角是
如图，已知等腰三角形ABC，顶点A的坐标是（
如图所示，已知等腰三角形ABC的底边BC=20cm，D是腰AB上一点，且CD=16cm，BD=12cm，求△ABC的周长．