题目内容
在不透明的口袋中，有四个形状、大小、质地完全相同的小球，四个小球上分别标有数字
，2，4，-
，现从口袋中任取一个小球，并将该小球上的数字作为平面直角坐标系中点P的横坐标，且点P在反比例函数y=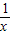
图象上，则点P落在正比例函数y=x图象上方的概率是 ．
【答案】分析：首先由点P在反比例函数y=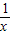
图象上，即可求得点P的坐标，然后找到点P落在正比例函数y=x图象上方的有几个，根据概率公式求解即可．
解答：解：∵点P在反比例函数y=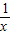
图象上，
∴点P的坐标可能为：（
，2），（2，
），（4，
），（-
，-3），
∵点P落在正比例函数y=x图象上方的有：（
，2），
∴点P落在正比例函数y=x图象上方的概率是
．
故答案为：
．
点评：此题考查了反比例函数与一次函数与点的关系，以及概率公式的应用．注意概率=所求情况数与总情况数之比．
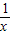图象上，即可求得点P的坐标，然后找到点P落在正比例函数y=x图象上方的有几个，根据概率公式求解即可．解答：解：∵点P在反比例函数y=
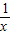图象上，∴点P的坐标可能为：（
，2），（2，），（4，），（-，-3），∵点P落在正比例函数y=x图象上方的有：（
，2），∴点P落在正比例函数y=x图象上方的概率是
．故答案为：
．点评：此题考查了反比例函数与一次函数与点的关系，以及概率公式的应用．注意概率=所求情况数与总情况数之比．
练习册系列答案
金版课堂课时训练系列答案
单元全能练考卷系列答案
新黄冈兵法密卷系列答案
相关题目