题目内容
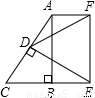
 如图,在长方形ABCD中AB=2acm,AD=3acm,△DGF是等腰三角形,求出阴影部分的面积S,并求出当a=4cm时,S的值是多少?(结果保留π)
如图,在长方形ABCD中AB=2acm,AD=3acm,△DGF是等腰三角形,求出阴影部分的面积S,并求出当a=4cm时,S的值是多少?(结果保留π)
解:∵AB=AG=CD=2acm,AD=3acm,
∴DG=DF=acm,
∴CE=CF=acm,
∴S=2a•3a- a2-
a2- -
-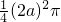
=( -
-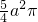 )cm2
)cm2
当a=4cm时,S=(88-20π)cm2
分析:根据阴影部分的面积等于矩形面积减去直角三角形和两个扇形的面积即可.
点评:本题考查了列代数式的知识,明确阴影部分的面积是由几个图形符合而成是解决本题的关键,另外也应熟悉扇形的面积计算方法.
∴DG=DF=acm,
∴CE=CF=acm,
∴S=2a•3a-
 a2-
a2- -
-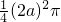
=(
 -
-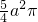 )cm2
)cm2当a=4cm时,S=(88-20π)cm2
分析:根据阴影部分的面积等于矩形面积减去直角三角形和两个扇形的面积即可.
点评:本题考查了列代数式的知识,明确阴影部分的面积是由几个图形符合而成是解决本题的关键,另外也应熟悉扇形的面积计算方法.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案
相关题目
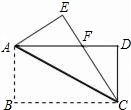 于点F.
于点F.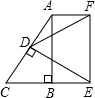 如图,在Rt△ABC中,∠ABC=90°,∠C=60°,BC=2,D是AC的中点,以D作DE⊥AC与CB的延长线交于E,以AB、BE为邻边作长方形ABEF,连接DF,求DF的长.
如图,在Rt△ABC中,∠ABC=90°,∠C=60°,BC=2,D是AC的中点,以D作DE⊥AC与CB的延长线交于E,以AB、BE为邻边作长方形ABEF,连接DF,求DF的长.