题目内容
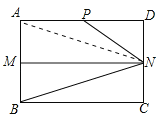
【题目】如图,在矩形ABCD中,AB=4,AD=6.M、N分别是AB、CD边的中点,P是AD上的点,且∠PNB=3∠CBN.
(1)求证:∠PNM=2∠CBN;
(2)求线段AP的长.

【答案】(1)证明见解析;(2)AP=![]() .
.
【解析】试题分析:(1)因为MN∥BC,可得∠CBN=∠MNB,由∠PNB=3∠CBN,根据角的和差不难得出结论;
(2)连接AN,由矩形的轴对称性,可得∠PAN=∠CBN,由(1)可知∠PNM=2∠CBN=2∠PAN,由AD∥MN,可得∠PAN=∠ANM,所以∠PAN=∠PNA,根据等角对等边得到AP=PN,再用勾股定理列方程求出AP.
试题解析:(1)∵四边形ABCD是矩形,M,N分别是AB,CD的中点,∴MN∥BC,∴∠CBN=∠MNB,∵∠PNB=3∠CBN,∴∠PNM=2∠CBN;
(2)连接AN,根据矩形的轴对称性,可知∠PAN=∠CBN,∵MN∥AD,∴∠PAN=∠ANM,由(1)知∠PNM=2∠CBN,∴∠PAN=∠PNA,∴AP=PN,∵AB=CD=4,M,N分别为AB,CD的中点,∴DN=2,设AP=x,则PD=6﹣x,在Rt△PDN中, ![]() ,∴
,∴![]() ,解得:x=
,解得:x=![]() ,所以AP=
,所以AP=![]() .
.

练习册系列答案
相关题目
【题目】为了更好营造班级的学习氛围,某中学对九年级六个班有关中考备考宣传墙报进行评比,评分如下:
班级 | 九(1) | 九(2) | 九(3) | 九(4) | 九(5) | 九(6) |
得分 | 95 | 94 | 91 | 90 | 88 | 88 |
(1)求出各班得分的极差、众数、平均数;
(2)本次评比设一、二、三奖,各班均能获奖,具体要求:一等奖的得分>二等奖的得分>三等奖的得分,一等奖的名额不能超过2个,三等奖的名额不能少于2个。若从上述方案中任选一种进行评奖,用列举法求出九(3)班获二等奖的概率.