题目内容
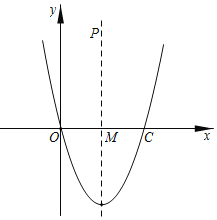
【题目】已知抛物线顶点坐标为(2,﹣4),且与x轴交于原点和点C,对称轴与x轴交点为M.
(1)求抛物线的解析式;
(2)A点在抛物线上,且A点的横坐标为﹣2,在抛物线对称轴上找一点B,使得AB与CB的差最大,求B点的坐标;
(3)P点在抛物线的对称轴上,且P点的纵坐标为8.探究:在抛物线上是否存在点Q使得O、M、P、Q四点共圆,若存在求出Q点坐标;若不存在请说明理由.
【答案】(1)抛物线的解析式为y=x2﹣4x;(2)点B(2,﹣12);(3)Q(5,5)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
【解析】
(1)根据顶点设出顶点坐标,再将原点的坐标代入即可得出答案;
(2)先求出A的坐标,根据三角形边的性质得出点O,A的直线与抛物线的对称轴的交点为点B,写出OA的解析式,即可得出答案;
(3)根据题意求出点P的坐标,根据四点共圆得出点Q在Rt△OMP外接圆上并设出Q的坐标,结合函数解析式以及点Q到OP的中点的距离列出方程组,解方程组,即可得出答案.
解:(1)∵抛物线顶点坐标为(2,﹣4),
∴设抛物线的解析式为y=a(x﹣2)2﹣4,
∵抛物线过原点,
∴0=a(0﹣2)2﹣4,
∴a=1,
∴抛物线的解析式为y=(x﹣2)2﹣4=x2﹣4x;
(2)由(1)知,抛物线的解析式为y=x2﹣4x,
令y=0,则x2﹣4x=0,
∴x=0或x=4,
∴C(4,0),
∵A点的横坐标为﹣2,
∴y=4﹣4×(﹣2)=12,
∴A(﹣2,12),
而抛物线的对称轴为x=2,
∴点C(4,0)关于抛物线的对称轴x=2的对称点为O(0,0),
则过点O,A的直线与抛物线的对称轴的交点为点B,理由是三角形三边关系定理之两边之差小于第三边,
∵A(﹣2,12),
∴直线OA的解析式为y=﹣6x,
当x=2时,y=﹣12,
∴点B(2,﹣12);
(3)由(2)知,抛物线的对称轴为直线x=2,
∴P(2,8),
∵抛物线的对称轴与x轴交点为M,
∴M(2,0),
∴∠OMP=90°,
∵点O、M、P、Q四点共圆,则点Q在Rt△OMP外接圆上,
∴点Q到OP的中点的距离等于半径![]() OP=
OP=![]() ,而OP的中点坐标为(1,4),
,而OP的中点坐标为(1,4),
由(1)知,抛物线的解析式为y=x2﹣4x,设Q坐标为(m,n),则m2﹣4m=n①,
∴(m﹣1)2+(n﹣4)2=17②,
∴m2﹣2m+n2﹣8n=0,
而m2﹣2m+(m2﹣4m)2﹣8(m2﹣4m)=m2﹣2m+m2(m﹣4)2﹣8m(m﹣4)
=m[m﹣2+m(m﹣4)2﹣8(m﹣4)]=m[(m﹣5)+(m﹣5)(m﹣4)2+5(m﹣4)2﹣8(m﹣5)+3﹣8]
=m{(m﹣5)+(m﹣5)(m﹣4)2+5[(m﹣5)2+2(m﹣5)+1]﹣8(m﹣5)﹣5}
=m[(m﹣5)+(m﹣5)(m﹣4)2+5(m﹣5)2+10(m﹣5)﹣8(m﹣5)]
=m(m﹣5)[1+(m﹣4)2+5(m﹣5)+2]
=m(m﹣5)(m2﹣3m﹣6)
∴m(m﹣5)(m2﹣3m﹣6)=0,
∴m=0(舍)或m=5或m2﹣3m﹣6=0,
∴m=5或m=![]() ,
,
∴Q(5,5)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).

 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案 期末好成绩系列答案
期末好成绩系列答案