题目内容
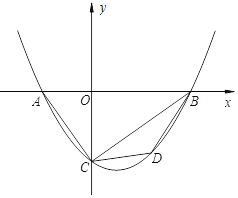
【题目】如图，抛物线y＝a（x+2）（x﹣4）与x轴交于A，B两点，与y轴交于点C，且∠ACO＝∠CBO．
（1）求线段OC的长度；
（2）若点D在第四象限的抛物线上，连接BD、CD，求△BCD的面积的最大值；
（3）若点P在平面内，当以点A、C、B、P为顶点的四边形是平行四边形时，直接写出点P的坐标．
【答案】（1）2
；（2）2；（3）(2，2)，(6，﹣2)或(﹣6，﹣2)
【解析】
（1）由抛物线的解析式先求出点A，B的坐标，再证△AOC∽△COB，利用相似三角形的性质可求出CO的长；
（2）先求出抛物线的解析式，再设出点D的坐标（m，
m2﹣
m﹣2），用含m的代数式表示出△BCD的面积，利用函数的性质求出其最大值；
（3）分类讨论，分三种情况由平移规律可轻松求出点P的三个坐标．
（1）在抛物线y＝a（x+2）（x﹣4）中，
当y＝0时，x1＝﹣2，x2＝4，
∴A（﹣2，0），B（4，0），
∴AO＝2，BO＝4，
∵∠ACO＝∠CBO，∠AOC＝∠COB＝90°，
∴△AOC∽△COB，
∴
，即
，
∴CO＝2；
（2）由（1）知，CO＝2，
∴C（0，﹣2）
将C（0，﹣2）代入y＝a（x+2）（x﹣4），
得，a＝，
∴抛物线解析式为：y＝x2﹣x﹣2，
如图1，连接OD，
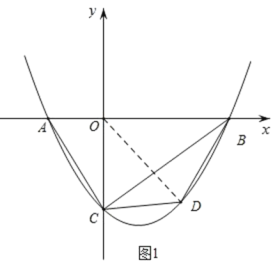
设D（m，m2﹣m﹣2），
则S△BCD＝S△OCD+S△OBD﹣S△BOC
＝
×2m+×4（﹣m2+m+2）﹣×4×2
＝﹣m2+2m
＝﹣（m﹣2）2+2，
根据二次函数的图象及性质可知，当m＝2时，△BCD的面积有最大值2；
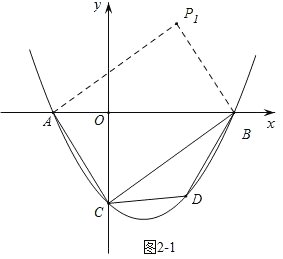
（3）如图2﹣1，当四边形ACBP为平行四边形时，由平移规律可知，点C向右平移4个单位长度，再向上平移2个单位长度得到点B，所以点A向右平移4个单位长度，再向上平移2个单位长度得到点P，因为A（﹣2，0），所以P1（2，2）；
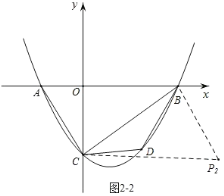
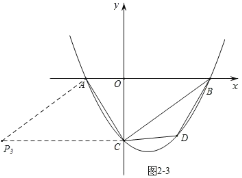
同理，在图2﹣2，图2﹣3中，可由平移规律可得P2（6，﹣2），P3（﹣6，﹣2）；
综上所述，当以点A、C、B、P为顶点的四边形是平行四边形时，点P的坐标为（2，2），（6，﹣2），P3（﹣6，﹣2）．
