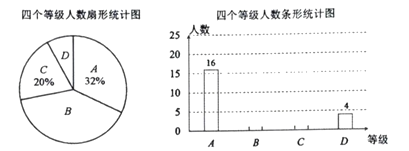
题目内容
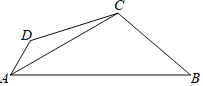
【题目】如图①,在矩形![]() 中,已知
中,已知![]() ,点
,点![]() 为
为![]() 边上一点,满足
边上一点,满足![]() ,动点
,动点![]() 以
以![]() 的速度沿线段
的速度沿线段![]() 从点
从点![]() 移动到点
移动到点![]() ,连接
,连接![]() ,作
,作![]() ,交线段
,交线段![]() 于点
于点![]() ,设点
,设点![]() 移动的时间为
移动的时间为![]() ,
,![]() 的长度为
的长度为![]() ,
,![]() 与
与![]() 的函数关系如图②所示.
的函数关系如图②所示.
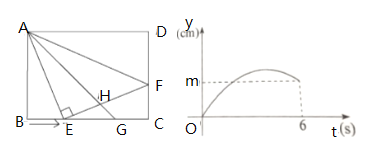
(1)图①中,![]() _______
_______![]() ,图②中,
,图②中,![]() _______;
_______;
(2)点![]() 能否为线段
能否为线段![]() 的中点?若可能,求出此时
的中点?若可能,求出此时![]() 的值,若不可能,请说明理由;
的值,若不可能,请说明理由;
(3)在图①中,连接![]() 、
、![]() ,设
,设![]() 与
与![]() 交于点
交于点![]() ,若
,若![]() 平分
平分![]() 的面积,求此时
的面积,求此时![]() 的值.
的值.
【答案】(1)2,2;(2)![]() 不能为
不能为![]() 中点;理由见解析;(3)
中点;理由见解析;(3)![]() .
.
【解析】
(1)可直接求出CG的长,证明![]() ,当t=6时,BE=6,即可求CF得长;
,当t=6时,BE=6,即可求CF得长;
(2)由![]() ,得到
,得到![]() ,即
,即![]() ,整理得,
,整理得,![]() ,
,
由当![]() 时,
时,![]() ,即可得出结论;
,即可得出结论;
(3)过![]() 作
作![]() 交
交![]() 于
于![]() ,如图,先证
,如图,先证![]() ,可得
,可得![]() ,
,![]() ,再证
,再证![]() ,列方程求解即可.
,列方程求解即可.
解:(1)图①中![]() ,
,![]()
∴CG=BC-AB=2,
∵∠B=∠C,∠AEB=∠EFC,
∴![]() ,
,
∴![]() ,
,
∴当t=6时,BE=6,
∴CF=2;
(2)∵![]()
∴![]() 即
即![]()
∴则![]()
∴![]()
∵当![]() 时,
时,![]()
∴![]() 不能为
不能为![]() 中点
中点
(3)过![]() 作
作![]() 交
交![]() 于
于![]() ,如图,
,如图,
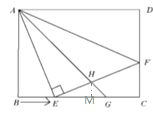
∵![]() 平分
平分![]() 的面积
的面积
∴![]() 为
为![]() 中点
中点
![]()
![]()
∴![]()
∴![]()
![]()
![]() 中,
中,![]()
∴![]()
∴![]()
即![]()
化简得![]()
![]() ,
,![]()
∵![]()
∴![]() .
.

练习册系列答案
相关题目