题目内容
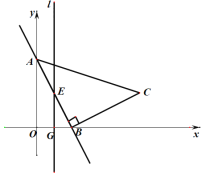
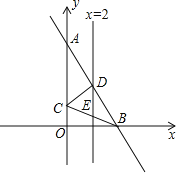
【题目】如图，平面直角坐标系中，直线AB：y=-2x+8交y轴于点A，交x轴于点B，以AB为底作等腰三角形△ABC的顶点C恰好落在y轴上，连接BC，直线x=2交AB于点D，交BC于点E，交x轴于点G，连接CD．
（1）求证：∠OCB=2∠CBA；
（2）求点C的坐标和直线BC的解析式；
（3）求△DEB的面积；
（4）在x轴上存在一点P使PD-PC最长，请直接写出点P的坐标．
【答案】(1)证明见解析；（2）C（0，3），直线BC解析式为y=-
x+3；（3）
；（4）P（-6，0）．
【解析】
（1）利用等腰三角形的性质和外角的性质可证得结论；
（2）可先求得A、B的坐标，则可求得OA=8、OB=4，在设OC=x，则AC=BC=8-x，在Rt△OBC中由勾股定理可列方程，可求得OC的长，则可求得点C的坐标，再利用待定系数法可求得直线BC的解析式；
（3）由直线AB、BC的解析式可分别求得点D、E的坐标，则可求得DE的长，可求得△DEB的面积；
（4）利用三角形三边关系可知PD-PC＜CD，当P、D、C三点在一条线上时，则有PD-PC=CD，此时其差最长，延长CD交x轴于点P，则该点即为P点，由C、D的坐标可求得直线CD的解析式，则可求得点P的坐标．
（1）证明：
∵△ABC为等腰三角形，
∴∠CAB=∠CBA，∠OCB为外角，
∴∠OCB=∠CAB+∠CBA，
∴∠OCB=2∠CBA；
（2）在y=-2x+8中，令x=0可得y=8，令y=0可求得x=4，
∴A（0，8），B（4，0），
∴OA=8，OB=4，
设OC=x，则AC=BC=8-x，
在Rt△OBC中，由勾股定理可得BC2=OC2+OB2，
即（8-x）2=x2+42，解得x=3，
∴C（0，3），
设直线BC解析式为y=kx+b，
把B、C点的坐标代入可得
，解得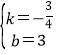
，
∴直线BC解析式为y=-x+3；
（3）直线x=2交AB于点D，交BC于点E，交x轴于点G，
∴D（2，4），E（2，
），G（2，0），
∴DE=4-=，且B（4，0），
∴BG=4-2=2，
∴S△DEB=
DEBG=××2=；
（4）∵PD-PC＜CD，
∴当P、D、C三点在一条线上时，则有PD-PC=CD，此时其差最长，
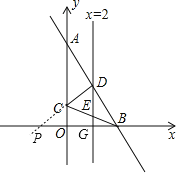
延长CD交x轴于点P，则该点即为P点，
设直线CD解析式为y=mx+n，
把C、D坐标代入可得
，解得
，
∴直线CD解析式为y=x+3，
令y=0可得x+3=0，解得x=-6，
∴P（-6，0）．
