题目内容
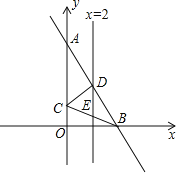
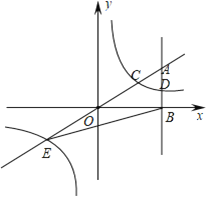
【题目】如图,在平面直角坐标系中,A点的坐标为(a,6),AB⊥x轴于点B,![]() =
=![]() ,反比例函数y=
,反比例函数y=![]() 的图象的一支分别交AO、AB于点C、D.延长AO交反比例函数的图象的另一支于点E.已知点D的纵坐标为
的图象的一支分别交AO、AB于点C、D.延长AO交反比例函数的图象的另一支于点E.已知点D的纵坐标为![]() .
.
(1)求反比例函数的解析式及点E的坐标;
(2)连接BC,求S△CEB.
(3)若在x轴上的有两点M(m,0)N(-m,0).
①以E、M、C、N为顶点的四边形能否为矩形?如果能求出m的值,如果不能说明理由.
②若将直线OA绕O点旋转,仍与y=![]() 交于C、E,能否构成以E、M、C、N为顶点的四边形为菱形,如果能求出m的值,如果不能说明理由.
交于C、E,能否构成以E、M、C、N为顶点的四边形为菱形,如果能求出m的值,如果不能说明理由.
【答案】(1)反比例函数的解析式为:y=![]() ;E(-4,-3);(2)24;(3)①m=5或-5.②以E、M、C、N为顶点的四边形不能为菱形.
;E(-4,-3);(2)24;(3)①m=5或-5.②以E、M、C、N为顶点的四边形不能为菱形.
【解析】
(1)根据已知条件可求A、D的坐标,用待定系数法即求出反比例函数解析式;由点A坐标求直线OA的解析式,把直线OA与反比例函数解析式联立方程组,即求出交点E;
(2)把△CEB分成△COB与△EOB,以OB为公共底,点C和点E纵坐标的绝对值为高即求出三角形面积;
(3)先由OC=OE,OM=ON得四边形EMCN为平行四边形.①若为矩形,则对角线相等,即MN=CE,易求出m的值;②若为菱形,则对角线互相垂直,但CE不与x轴垂直,矛盾,故不能成为菱形.
本题考查了反比例函数的图象与性质,反比例函数与一次函数的综合运用,平行四边形、矩形、菱形的判定.
(1)∵A点的坐标为(a,6),AB⊥x轴于B,
∴AB=6,
∵![]() ,
,
∴OB=8,
∴A(8,6),D(8,![]() ),
),
∵点D在反比例函数y=![]() 的图象上,
的图象上,
∴k=8×![]() =12,
=12,
∴反比例函数的解析式为:y=![]() ,
,
设直线OA的解析式为:y=bx,
∴8b=6,解得:b=![]() ,
,
∴直线OA的解析式为:y=![]() x,
x,
 解得:
解得:![]() ,
,![]() ,
,
∴E(-4,-3);
(2)由(1)可知C(4,3),E(-4,-3),B(8,0),
∴S△CEB=S△COB+S△EOB=![]() =
=![]() OB(yC+|yE|)=
OB(yC+|yE|)=![]() ×8×(3+3)=24;
×8×(3+3)=24;
(3)①以E、M、C、N为顶点的四边形能为矩形,
∵M(m,0),N(-m,0),
∴OM=ON,
∵
∴四边形EMCN是平行四边形,
当MN=CE=2OC=2×![]() =10时,EMCN为矩形,
=10时,EMCN为矩形,
∴OM=ON=5,
∴m=5或-5;
②∵CE所在直线OA不可能与x轴垂直,即CE不能与MN垂直,
∴以E、M、C、N为顶点的四边形不能为菱形.

 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案