题目内容
【题目】“垃圾不落地,商南更美丽”。某中学为了了解七年级学生对这个一倡议的落实情况,学校安排政教处在七年级学生中随机抽取了部分学生,并针对学生“是否随手丢垃圾”这一情况进行了问卷调查,将这一情况分为:![]() ——从不随手丢垃圾;
——从不随手丢垃圾;![]() ——偶尔随手丢垃圾;
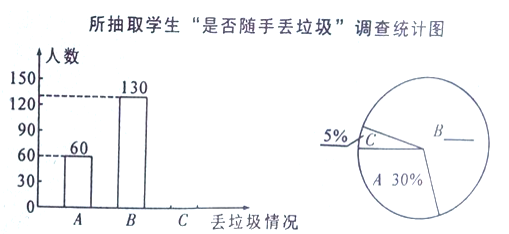
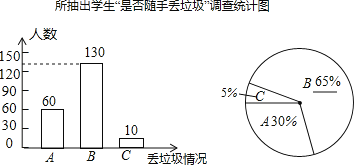
——偶尔随手丢垃圾;![]() ——经常随手丢垃圾三项。要求每位被调查的学生必须从以上三项中选一项且只能选一项。现将调查结果绘制成以下两幅不完整的统计图。请你根据以上信息,解答下列问题:
——经常随手丢垃圾三项。要求每位被调查的学生必须从以上三项中选一项且只能选一项。现将调查结果绘制成以下两幅不完整的统计图。请你根据以上信息,解答下列问题:
(1)补全条形统计图和扇形统计图;
(2)图中“偶尔随手丢垃圾”所在扇形的圆心角为______________;
(3)若该校七年级共有1500名学生,请你估计该年级学生中“经常随手丢垃圾”的学生约有多少人?谈谈你的看法?
【答案】(1)见解析;(2)234°;(3)75人,见解析.
【解析】
(1)根据A情况的人数及其所占百分比求得总人数,用总人数减去A、B人数求得C情况的人数,再用B情况人数除以总人数可得其百分比;
(2)根据统计图中的数据可以求得扇形统计图中B所在扇形的圆心角度数;
(3)总人数乘以样本中C情况的百分比可得.
解:(1)∵被调查的总人数为60÷30%=200人,
∴C情况的人数为200-(60+130)=10人,B情况人数所占比例为
![]() ×100%=65%,
×100%=65%,
补全图形如下:
 ;
;
(2)由(1)知B情况人数所占比例为65%,所以圆心角65%×![]() =
=![]() ;
;
(3)∵“经常随手丢垃圾”的学生所占比例为5%,
∴1500×5%=75(人),
答:估计该年级学生中“经常随手丢垃圾”的学生约有75人,就该年级经常随手丢垃圾的学生人数看出仍需要加强公共卫生教育、宣传和监督.

 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案【题目】口袋中装有四个大小完全相同的小球,把它们分别标号1,2,3,4,从中随机摸出一个球,记下数字后放回,再从中随机摸出一个球,利用树状图或者表格求出两次摸到的小球数和等于4的概率.
【答案】![]() .
.
【解析】试题分析:
根据题意列表如下,由表可以得到所有的等可能结果,再求出所有结果中,两次所摸到小球的数字之和为4的次数,即可计算得到所求概率.
试题解析:
列表如下:
1 | 2 | 3 | 4 | |
1 | (1,1) | (1,2) | (1,3) | (1,4) |
2 | (2,1) | (2,2) | (2,3) | (2,4) |
3 | (3,1) | (3,2) | (3,3) | (3,4) |
4 | (4,1) | (4,2) | (4,3) | (4,4) |
由表可知,共有16种等可能事件,其中两次摸到的小球数字之和等于4的有(3,1)、(2,2)和(1,3),共计3种,
∴P(两次摸到小球的数字之和等于4)=![]() .
.
【题型】解答题
【结束】
23
【题目】小亮同学想利用影长测量学校旗杆AB的高度,如图,他在某一时刻立1米长的标杆测得其影长为1.2米,同时旗杆的投影一部分在地面上BD处,另一部分在某一建筑的墙上CD处,分别测得其长度为9.6米和2米,求旗杆AB的高度.

【题目】某超市销售进价为2元的雪糕,在销售中发现,此商品的日销售单价x(元)与日销售量y(根)之间有如下关系:
日销售单价x(元) | 3 | 4 | 5 | 6 |
日销售量y(根) | 40 | 30 | 24 | 20 |
(1)猜测并确定y和x之间的函数关系式;
(2)设此商品销售利润为W,求W与x的函数关系式,若物价局规定此商品最高限价为10元/根,你是否能求出商品日销售最大利润?若能请求出,不能请说明理由.