题目内容
【题目】已知一次函数![]() 的图像与
的图像与![]() 轴、
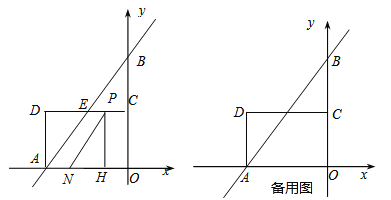
轴、![]() 轴分别交于点B、A.以AB为边在第一象限内作等腰直角三角形ABC,且∠ABC=90°,BA=BC,作OB的垂直平分线l,交直线AB与点E,交x轴于点G.
轴分别交于点B、A.以AB为边在第一象限内作等腰直角三角形ABC,且∠ABC=90°,BA=BC,作OB的垂直平分线l,交直线AB与点E,交x轴于点G.
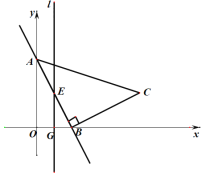
(1)求点![]() 的坐标;
的坐标;
(2)在OB的垂直平分线l上有一点M,且点M与点C位于直线AB的同侧,使得![]() ,求点M的坐标;
,求点M的坐标;
(3)在(2)的条件下,联结CE、CM,判断△CEM的形状,并给予证明;
【答案】(1) C(6,2);(2) M(1,7);(3)见解析.
【解析】
(1)过点C作x轴的垂线,交x轴于点H,通过“角边角”易证![]() ≌
≌![]() ,得到BH=AO=4,CH=OB=2,即可得到C点坐标;
,得到BH=AO=4,CH=OB=2,即可得到C点坐标;
(2)根据题意可设点M(1,a),根据![]() 可得关于m的方程,然后求解方程即可;
可得关于m的方程,然后求解方程即可;
(3)由(2)可得CE=5,EM=5,CM=![]() ,根据勾股定理的逆定理即可得到
,根据勾股定理的逆定理即可得到![]() 是等腰直角三角形.
是等腰直角三角形.
解:(1)过点C作x轴的垂线,交x轴于点H,

∵![]() ,
,
∴A(0,4),B(2,0),
∵BA=BC,
∴![]() ≌
≌![]() (ASA),
(ASA),
∴BH=AO=4,CH=OB=2,
∴C(6,2)
(2)如图,由题意可知点G(1,0),点E(1,2),
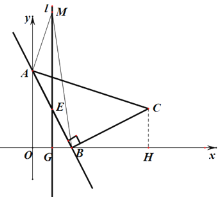
∵AB=BC=2![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
而![]() ,
,
设M(1,a),则![]() ,
,
解的a=7,
则M(1,7) ;
(3)联结CM,CE,
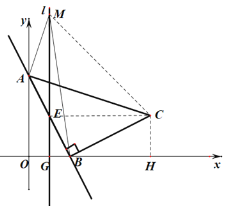
由于点E(1,2),C(6,2),M(1,7),
则CE=5,EM=5,CM=![]() ,
,
可得:![]() ,
,
CE=EM,
∴![]() 是等腰直角三角形.
是等腰直角三角形.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目