Question

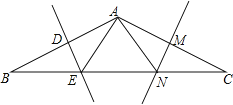
【题目】如图，点P是以O为圆心，AB为直径的半圆的中点，AB=2，等腰直角三角板45°角的顶点与点P重合，当此三角板绕点P旋转时，它的斜边和直角边所在的直线与直径AB分别相交于C，D两点．设线段AD的长为x，线段BC的长为y，则下列图象中，能表示y与x的函数关系的图象大致是（ ）

A.
B.
C.
D.

Answer 1

【答案】C
【解析】解：如图，连接AP、BP，
∵点P是以O为圆心，AB为直径的半圆的中点，
∴∠APB=90°，∠A=∠ABP=45°，
把△ACP绕点P逆时针旋转90°得到△BPE，
则PC=PE，∠PBE=∠A=45°，
∴∠DBE=∠ABP+∠PBE=45°+45°=90°，
∵∠CPD=45°，
∴∠DPE=∠DPC=45°，
在△PCD和△PED中，
，
∴△PCD≌△PED（SAS），
∴DE=CD，
∵AB=2，AD=x，BC=y，
∴BE=AC=2﹣y，BD=2﹣x，
CD=AB﹣AC﹣BD=2﹣（2﹣y）﹣（2﹣x）=x+y﹣2，
在Rt△DBE中，BD2+BE2=DE2 ，
即（2﹣x）2+（2﹣y）2=（x+y﹣2）2 ，
整理得，y= ，
纵观各选项，只有C选项图形符合．
故选C．