题目内容
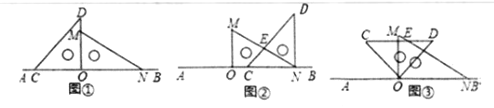
【题目】如图1,将一副直角三角板放在同一条直线AB上,其中∠ONM=30![]() ,∠OCD=45
,∠OCD=45![]()
(1)观察猜想
将图1中的三角尺OCD沿AB的方向平移至图②的位置,使得点O与点N重合,CD与MN相交于点E,则∠CEN= ![]() .
.
(2)操作探究
将图1中的三角尺OCD绕点O按顺时针方向旋转,使一边OD在∠MON的内部,如图3,且OD恰好平分∠MON,CD与NM相交于点E,求∠CEN的度数;
(3)深化拓展
将图1中的三角尺OCD绕点O按沿顺时针方向旋转一周,在旋转的过程中,当边OC旋转 ![]() 时,边CD恰好与边MN平行。(直接写出结果)
时,边CD恰好与边MN平行。(直接写出结果)
【答案】(1)105°;(2)150°;(3)75°或255°
【解析】
分析: (1)根据三角形的内角和定理可得∠CEN=180°-∠DCN-∠MNO,代入数据计算即可得解;
(2)根据角平分线的定义求出∠DON=45°,利用内错角相等两直线平行求出CD∥AB,再根据两直线平行,同旁内角互补求解即可;
(3)①分CD在AB上方时,CD∥MN,设OM与CD相交于F,根据两直线平行,同位角相等可得∠OFD=∠M=60°,然后根据三角形的内角和定理列式求出∠MOD,即可得解;CD在AB的下方时,CD∥MN,设直线OM与CD相交于F,根据两直线平行,内错角相等可得∠DFO=∠M=60°,然后利用三角形的内角和定理求出∠DOF,再求出旋转角即可;②分CD在OM的右边时,设CD与AB相交于G,根据直角三角形两锐角互余求出∠CGN,再根据三角形的一个外角等于与它不相邻的两个内角的和求出∠CON,再求出旋转角即可,CD在OM的左边时,设CD与AB相交于G,根据直角三角形两锐角互余求出∠NGD,再根据三角形的一个外角等于与它不相邻的两个内角的和列式求出∠AOC,然后求出旋转角,计算即可得解.
详解:
(1)105°;
(2)∵OD平分∠MON,
∴∠DON=![]() ∠MPN=
∠MPN=![]() ×90°=45°,
×90°=45°,
∴∠DON=∠D=45°,
∴CD∥AB,
∴∠CEN=180°﹣∠MNO=180°﹣30°=150°;
(3)75°或255°时,边CD恰好与边MN平行.

 字词句段篇系列答案
字词句段篇系列答案【题目】在一个不透明的盒子里装着除颜色外完全相同的黑、白两种小球共40个,小明做摸球实验,他将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是实验中的一组统计数据:
摸球的次数n | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
摸到白球的次数m | 70 | 128 | 171 | 302 | 481 | 599 | 903 |
摸到白球的频率 | 0.75 | 0.64 | 0.57 | 0.604 | 0.601 | 0.599 | 0.602 |
(1)请估计:当n很大时,摸到白球的概率约为 .(精确到0.1)
(2)估算盒子里有白球 个.
(3)若向盒子里再放入x个除颜色以外其它完全相同的球,这x个球中白球只有1个,每次将球搅拌均匀后,任意摸出一个球记下颜色再放回,通过大量重复摸球试验后发现,摸到白球的频率稳定在50%,那么可以推测出x最有可能是 .
【题目】中华文明,源远流长;中华汉字,寓意深广,为传承中华优秀传统文化,某校团委组织了一次全校3000名学生参加的“汉字听写大赛”![]() 为了解本次大赛的成绩,校团委随机抽取了其中若干名学生的成绩作为样本进行统计,制成如下不完整的统计图表:
为了解本次大赛的成绩,校团委随机抽取了其中若干名学生的成绩作为样本进行统计,制成如下不完整的统计图表:
成绩 | 频数 | 频率 |
| 10 |
|
| 30 |
|
| 40 | n |
| m |
|
| 50 |
|
a | 1 |
请根据所给信息,解答下列问题:
![]() ______,
______,![]() ______,
______,![]() ______;
______;
![]() 补全频数直方图;
补全频数直方图;
![]() 这若干名学生成绩的中位数会落在______分数段;
这若干名学生成绩的中位数会落在______分数段;
![]() 若成绩在90分以上
若成绩在90分以上![]() 包括90分
包括90分![]() 的为“优”等,请你估计该校参加本次比赛的3000名学生中成绩是“优”等的约有多少人?
的为“优”等,请你估计该校参加本次比赛的3000名学生中成绩是“优”等的约有多少人?