Question

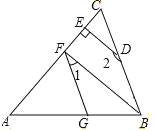
【题目】△ABC中，∠ACB=90°，CD⊥AB于D，AE平分∠CAB交CD于F，CH⊥EF于H，连接DH，求证：(1)EH=FH；

(2)∠CAB=2∠CDH．

Answer 1

【答案】（1）证明见解析（2）证明见解析

【解析】试题分析：（1）根据余角的性质得到∠AFD＝∠AEC，证得∠CFE＝∠CEF，得到CF＝CE，根据等腰三角形的性质即可得到结论．

（2）由于∠ADF＝∠CHF＝90°，∠AFD＝∠CFH，得到△ADF∽△CFH，根据相似三角形的性质得到，由于∠AFC＝∠DFH，得到△AFC∽△DFH，根据相似三角形的性质得到∠CAF＝∠CDH，等量代换即可得到结论．

试题解析：

（1）证明：∵∠ACB＝90°，CD⊥AB于D，

∴∠CAE+∠AEC＝∠DAF+∠AFD＝90°，

∵AE平分∠CAB，

∴∠CAE＝∠DAF，

∴∠AFD＝∠AEC，

∵∠AFD＝∠CFE，

∴∠CFE＝∠CEF，

∴CF＝CE，

∵CH⊥EF，

∴HE＝HF；

（2）证明：∵∠ADF＝∠CHF＝90°，∠AFD＝∠CFH，

∴△ADF∽△CFH，

∴，

∵∠AFC＝∠DFH，

∴△AFC∽△DFH，

∴∠CAF＝∠CDH，

∵∠CAD＝2∠CAF，

∴∠CAB＝2∠CDH．