��Ŀ����
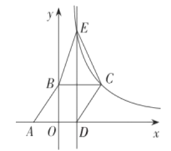
����Ŀ����ͼ��AB��ԲO��ֱ������C��ԲO��һ�㣬��CAB��30�㣬D��ֱ��AB��һ���㣬����CD������D��CD�Ĵ��ߣ���ԲO������һ�������Ϊ��E����Eλ��ֱ��CD�Ϸ�����ࣩ������EC����֪AB��6cm����A��D�����ľ���Ϊxcm��C��D�����ľ���Ϊy1cm��E��C�����ľ���Ϊy2cm��Сѩ����ѧϰ�����ľ��飬�ֱ�Ժ���y1��y2���Ա���x�ı仯���仯�Ĺ��ɽ�����̽����������Сѩ��̽�����̣�
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y1/cm | 5.2 | 4.4 | 3.6 | 3.0 | 2.7 | 2.7 | �� �� |
y2/cm | 5.2 | 4.6 | 4.2 | �� �� | 4.8 | 5.6 | 6.0 |
��1�������±����Ա���x��ֵ����ȡ�㡢��ͼ���������ֱ�õ���y1��y2��x�ļ����Ӧֵ���뽫����������������һλС����
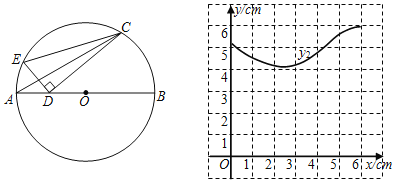
��2����ͬһƽ��ֱ������ϵxOy�У�y2��ͼ����ͼ��ʾ�������ȫ��ı��и�����ֵ����Ӧ�ĵ㣨x��y1������x��y2��������������y1��ͼ��
��3����Ϻ���ͼ������⣺����ECD��60��ʱ��AD�ij���ԼΪ�� ��cm��
���𰸡���1��4.2��3.0����2�������������3��4.5��6.0��
��������
��1����x��3ʱ����D���O�غϣ���ʱ��DCE�ǵ���ֱ�������Σ���x��6ʱ����D��B�غϣ��ɴ˼��ɽ�����⣻
��2��������㷨��������ͼ�ɣ�
��3������ֱ��������30�Ƚǵ����ʿ�֪��EC��2CD���Ƴ�y2��2y1���۲캯��ͼ���֪������������x��ֵΪ4.5cm��6cm��
�⣺��1����x��3ʱ����AB��6��AD��3��
���D���O�غϣ���ʱ��DCE�ǵ���ֱ�������Σ�
��CD��DE��3��
��y2��![]() ��4.2��
��4.2��
��x��6ʱ����D��B�غϣ�
��CD��BC��
�ߡ�CAB��30�㣬
��CD��BC��![]() AB��3.0��
AB��3.0��
�ʴ�Ϊ��4.2��3.0��
��2������ͼ����ͼ��ʾ��

��3������ECD��60��ʱ��
��Rt��ECD�У��ߡ�EDC��90�㣬
���CED��30�㣬
��EC��2CD��
��y2��2y1��
�۲�ͼ���֪������������x��ֵΪ4.5cm��6.0cm��
�ʴ�Ϊ��4.5��6.0��

 �����������һ��һ��ϵ�д�
�����������һ��һ��ϵ�д�