题目内容
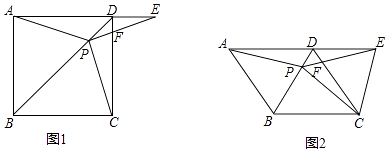
【题目】如图,在边长为4的正方形ABCD中,点E是边CD的中点,AE的垂直平分线交边BC于点G,交边AE于点F,连接DF,EG,以下结论:①DF= ![]() ,②DF∥EG,③△EFG≌△ECG,④BG=
,②DF∥EG,③△EFG≌△ECG,④BG= ![]() ,正确的有:(填写序号)
,正确的有:(填写序号)
【答案】①④
【解析】解:如图,设FG交AD于M,连接BE.
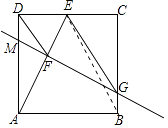
∵四边形ABCD是正方形,
∴AB=BC=CD=AD=4,∠ADC=∠C=90°,
∵DE=EC=2,
在Rt△ADE中,AE= ![]() =
= ![]() =2
=2 ![]() .
.
∵AF=EF,
∴DF= ![]() AE=
AE= ![]() ,故①正确,
,故①正确,
易证△AED≌△BEC,
∴∠AED=∠BEC,
∵DF=EF,
∴∠FDE=∠FED=∠BEC,
∴DF∥BE,
∵BE与EG相交,
∴DF与EG不平行,故②错误,
∵AE⊥MG,易证AE=MG=2 ![]() ,
,
由△AFM∽△ADE,可知 ![]() =
= ![]() ,
,
∴FM= ![]() ,FG=
,FG= ![]() ,
,
在Rt△EFG中,EG= ![]() =
= ![]() ,
,
在Rt△ECG中,CG= ![]() =
= ![]() ,
,
∴BG=BC﹣CG=4﹣ ![]() =
= ![]() ,故④正确,
,故④正确,
∵EF≠EC,FG≠CG,∴△EGF与△EGC不全等,故③错误,
所以答案是①④.
【考点精析】利用线段垂直平分线的性质和正方形的性质对题目进行判断即可得到答案,需要熟知垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等;正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.

【题目】某校为了解八年级学生的视力情况,对八年级的学生进行了一次视力调查,并将调查数据进行统计整理,绘制出如下频数分布表和频数分布直方图的一部分.
视力 | 频数(人) | 频率 |
4.0≤x<4.3 | 20 | 0.1 |
4.3≤x<4.6 | 40 | 0.2 |
4.6≤x<4.9 | 70 | 0.35 |
4.9≤x<5.2 | a | 0.3 |
5.2≤x<5.5 | 10 | b |
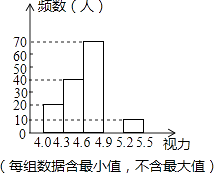
(1)在频数分布表中,a= , b=;
(2)将频数分布直方图补充完整;
(3)若视力在4.6以上(含4.6)均属正常,求视力正常的人数占被调查人数的百分比是多少?