题目内容
【题目】如图1,在正方形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,且PA=PE,PE交CD于F.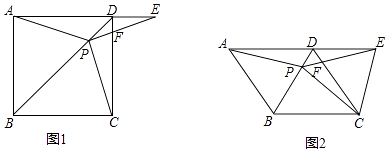
(1)求证:PC=PE;
(2)图1中与∠EAP相等的角是和 , 则可求∠CPE=°;
(3)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=120°,连接CE,请直接写出∠CPE=°.
【答案】
(1)证明:∵四边形ABCD为正方形,
∴BA=BC,∠ABD=∠CBD=45°,
在△ABP和△CBP中
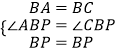 ,
,
∴△ABP≌△CBP,
∴PA=PC,
∵PA=PE,
∴PC=PE;
(2)∠E,∠PCD,90
(3)60
【解析】(2)解:∵△ABP≌△CBP,
∴∠PAB=∠PCB,
∴∠PAD=∠PCD,
∵PA=PE,
∴∠PAE=∠E,
∴∠PCD=∠E,
而∠DFE=∠PFC,
∴∠CPF=∠EDF=90°,
即图1中与∠EAP相等的角是∠E和∠PCD;
⑶∵四边形ABCD为菱形,
∴BA=BC,∠ABD=∠CBD=60°,∠ADC=∠ABC=120°,
∴∠EDC=60°,
在△ABP和△CBP中
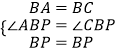 ,
,
∴△ABP≌△CBP,
∴PA=PC,∠PAB=∠PCB,
∴∠PAD=∠PCD,
∵PA=PE,
∴∠PAD=∠PED,
∴∠PCD=∠PED,
而∠DFE=∠PFC,
∴∠CPF=∠EDF=60°.
故答案为∠E,∠PCD,90,60.
(1)四边形ABCD为正方形,得到BA=BC,∠ABD=∠CBD=45°,△ABP≌△CBP,得到PA=PC,由PA=PE,得到PC=PE;(2)由△ABP≌△CBP,得到∠PAB=∠PCB,∠PAD=∠PCD,由PA=PE,得到∠PAE=∠E,∠PCD=∠E,而∠DFE=∠PFC,得到∠CPF=∠EDF=90°,即图1中与∠EAP相等的角是∠E和∠PCD;⑶由四边形ABCD为菱形,得到BA=BC,∠ABD=∠CBD=60°,∠ADC=∠ABC=120°,∠EDC=60°,△ABP≌△CBP,得到PA=PC,∠PAB=∠PCB,∠PAD=∠PCD,由PA=PE,得到∠PAD=∠PED,∠PCD=∠PED,而∠DFE=∠PFC,得到∠CPF=∠EDF=60°;故答案为∠E,∠PCD,90,60.

 全能测控一本好卷系列答案
全能测控一本好卷系列答案