题目内容
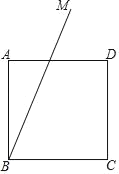
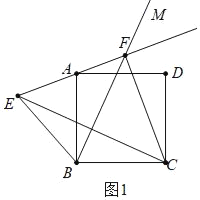
【题目】在正方形ABCD的内侧作直线BM,点C关于BM的对称点为E,直线BM与EA的延长线交于点F,连接BE、CE、CF.
(1)依题意补全图形;
(2)求证:CF⊥EF;
(3)直接写出线段AB、EF、AF之间的数量关系.
【答案】(1)详见解析;(2)详见解析;(3)EF2+AF2=2AB2
【解析】
(1)依题意画图;
(2)由BE=BE=BC构造出E、A、C在以B为圆心的圆上,利用同弧所对的圆周角等于圆心角的一半,得出∠FEC=45°由FB是EC的垂直平分线推出等腰△EFC,得出∠FEC=∠FCE=45°,由三角形内角和推出∠EFC=90°,得出结论;
(3)利用勾股定理:![]() 得出
得出![]() 由于
由于![]() 得出结论。
得出结论。
解:(1)图形如图1中所示:
(2)如图2中,
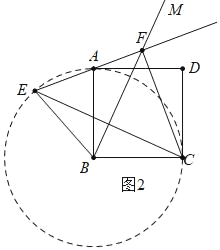
∵BE=BE=BC,
∴E、A、C在以B为圆心BC为半径的⊙B上,
∵四边形ABCD是正方形,
∴∠ABC=90°,
∴∠FEC=![]() ∠ABC=45°,
∠ABC=45°,
∵BM是线段EC的垂直平分线,
∴FE=FC,
∴∠FEC=∠FCE=45°,
∴∠EFC=90°,即EF⊥CF.
(3)如图3中,结论:![]() .
.
理由:连接AC.
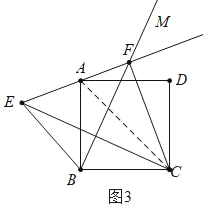
∵∠AFC=∠ABC=90°,
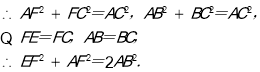

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
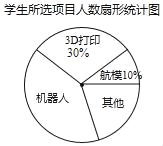
小学生10分钟应用题系列答案【题目】初一(1)班针对“你最喜爱的课外活动项目”对全班学生进行调查(每名学生分别选一个活动项目),并根据调查结果列出统计表,绘制成扇形统计图.
男、女生所选项目人数统计表
项目 | 男生(人数) | 女生(人数) |
机器人 | 7 | 9 |
3D打印 | m | 4 |
航模 | 2 | 2 |
其他 | 5 | n |
根据以上信息解决下列问题:
(1)m=_____,n=_____;
(2)扇形统计图中机器人项目所对应扇形的圆心角度数为_____°;
(3)从选航模项目的4名学生中随机选取2名学生参加学校航模兴趣小组训练,请用列举法(画树状图或列表)求所选取的2名学生中恰好有1名男生、1名女生的概率.
【题目】某社区超市第一次用6000元购进甲、乙两种商品,其中乙商品的件数比甲商品件数的![]() 倍多15件,甲、乙两种商品的进价和售价如下表:(注:获利=售价﹣进价)
倍多15件,甲、乙两种商品的进价和售价如下表:(注:获利=售价﹣进价)
甲 | 乙 | |
进价(元/件) | 22 | 30 |
售价(元/件) | 29 | 40 |
(1)该超市购进甲、乙两种商品各多少件?
(2)该超市将第一次购进的甲、乙两种商品全部卖完后一共可获得多少利润?
(3)该超市第二次以第一次的进价又购进甲、乙两种商品,其中甲商品的件数不变,乙商品的件数是第一次的3倍;甲商品按原价销售,乙商品打折销售,第二次两种商品都销售完以后获得的总利润比第一次获得的总利润多180元,求第二次乙商品是按原价打几折销售?