题目内容
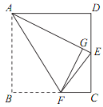
【题目】如图，在正方形纸片 ABCD 中， E 是 CD 的中点，将正方形纸片折叠，点 B 落在线段AE 上的点 G 处，折痕为 AF ．若 AD＝4 cm，则 CF 的长为___________cm ．
【答案】
【解析】
设BF=x，则FG=x，CF=4-x，在Rt△GEF中，利用勾股定理可得EF2=（2
-4）2+x2，在Rt△FCE中，利用勾股定理可得EF2=（4-x）2+22，从而得到关于x方程，求解x，最后用4-x即可．
设BF=x，则FG=x，CF=4-x．
在Rt△ADE中，利用勾股定理可得AE=2．
根据折叠的性质可知AG=AB=4，所以GE=2-4．
在Rt△GEF中，利用勾股定理可得EF2=（2-4）2+x2，
在Rt△FCE中，利用勾股定理可得EF2=（4-x）2+22，
所以（2-4）2+x2=（4-x）2+22，
解得x=2-2．
则FC=4-x=6-2．
故答案为：6-2．
【题目】为了解学生每天的睡眠情况，某初中学校从全校 800 名学生中随机抽取了 40 名学生，调查了他们平均每天的睡眠时间（单位： h） ，统计结果如下：
9，8，10.5，7，9，8，10，9.5，8，9，9.5，7.5，9.5，9，8.5，7.5，10，9.5，8，9，
7，9.5，8.5，9，7，9，9，7.5，8.5，8.5，9，8，7.5，9.5，10，9.5，8.5，9，8，9.
在对这些数据整理后，绘制了如下的统计图表：
睡眠时间分组统计表 睡眠时间分布情况
组别 | 睡眠时间分组 | 人数（频数） |
1 | 7≤t＜8 | m |
2 | 8≤t＜9 | 11 |
3 | 9≤t＜10 | n |
4 | 10≤t＜11 | 4 |
请根据以上信息，解答下列问题：
（1） m = ， n = ， a = ， b = ；
（2）抽取的这 40 名学生平均每天睡眠时间的中位数落在 组（填组别） ；
（3）如果按照学校要求，学生平均每天的睡眠时间应不少于 9 h，请估计该校学生中睡眠时间符合要求的人数．
