题目内容
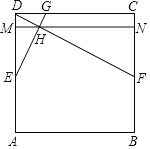
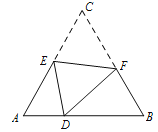
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() .点
.点![]() 由点
由点![]() 出发沿
出发沿![]() 方向向点
方向向点![]() 匀速运动,同时点
匀速运动,同时点![]() 由点
由点![]() 出发沿
出发沿![]() 方向向点
方向向点![]() 匀速运动,它们的速度均为
匀速运动,它们的速度均为![]() .作
.作![]() 于
于![]() ,连接
,连接![]() ,设运动时间为
,设运动时间为![]() ,解答下列问题:
,解答下列问题:
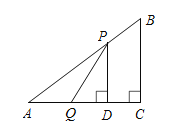
(1)设![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 之间的函数关系式,
之间的函数关系式,![]() 的最大值是 ;
的最大值是 ;
(2)当![]() 的值为 时,
的值为 时,![]() 是等腰三角形.
是等腰三角形.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() 或
或![]()
【解析】
(1)先通过条件求出![]() ,再利用对应边成比例求出PD,再利用面积公式写出式子,再根据顶点公式求最大值即可.
,再利用对应边成比例求出PD,再利用面积公式写出式子,再根据顶点公式求最大值即可.
(2)分别讨论AQ=AP时, AQ=PQ时, AP=PQ时的三种情况.
解(1)![]() ,
,
![]() ,
,
又![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 的最大值是
的最大值是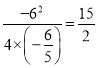 .
.
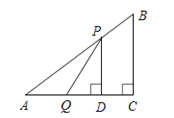
(2)由(1)知:AQ=2t,AP=10-2t,
①当AQ=AP时,即2t=10-2t,解得t=![]() .
.
②当AQ=PQ时,作QE⊥AP,如图所示,
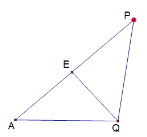
根据等腰三角形的性质,AE=![]() ,
,
易证Rt△AQE∽Rt△ACB,
∴![]() ,即
,即![]() ,解得t=
,解得t=![]() .
.
③当AP=PQ时,作PF⊥AQ,如图所示,
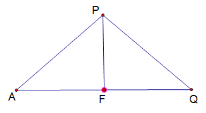
根据等腰三角形的性质,AF=![]() ,
,
易证Rt△AFP∽Rt△ACB,
∴![]() ,即
,即![]() ,解得t=
,解得t=![]() .
.
综上所述,t=![]() 或
或![]() 或
或![]() .
.

练习册系列答案
相关题目
【题目】某校为了解七、八年级学生英语听力训练情况(七、八年级学生人数相同),某周从这两个年级学生中分别随机抽查了30名同学,调查了他们周一至周五的听力训练情况,根据调查情况得到如下统计图表:
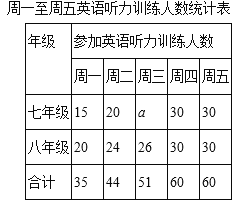

(1)填空:a= ;
(2)根据上述统计图表完成下表中的相关统计量:
年级 | 平均训练时间的中位数 | 参加英语听力训练人数的方差 |
七年级 | 24 | 34 |
八年级 |
| 14.4 |
(3)请你利用上述统计图表对七、八年级英语听力训练情况写出两条合理的评价;
(4)请你结合周一至周五英语听力训练人数统计表,估计该校七、八年级共480名学生中周一至周五平均每天有多少人进行英语听力训练.