ЬтФПФкШн
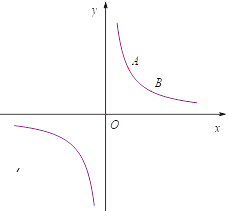
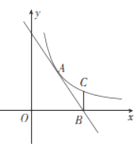
ЁОЬтФПЁПЖдгкЦНУцЩЯAЁЂBСНЕуЃЌИјГіШчЯТЖЈвхЃКвдЕуAЮЊжааФЃЌBЮЊЦфжавЛИіЖЅЕуЕФе§ЗНаЮГЦЮЊЕуAЁЂBЕФЁАСьгђЁБЃЎ
ЃЈ1ЃЉвбжЊЕуAЕФзјБъЮЊЃЈЉ1ЃЌ1ЃЉЃЌЕуBЕФзјБъЮЊЃЈ3ЃЌ3ЃЉЃЌЖЅЕуAЁЂBЕФЁАСьгђЁБЕФУцЛ§ЮЊЁЁ ЁЁЃЎ
ЃЈ2ЃЉШєЕуAЁЂBЕФЁАСьгђЁБЕФе§ЗНаЮЕФБпгызјБъжсЦНааЛђДЙжБЃЌЛиД№ЯТСаЮЪЬтЃК
ЂйвбжЊЕуAЕФзјБъЮЊЃЈ2ЃЌ0ЃЉЃЌШєЕуAЁЂBЕФЁАСьгђЁБЕФУцЛ§ЮЊ16ЃЌЕуBдкxжсЩЯЗНЃЌЧѓBЕузјБъЃЛ
ЂквбжЊЕуAЕФзјБъЮЊЃЈ2ЃЌmЃЉЃЌШєдкжБЯпlЃКyЃНЉ3x+2ЩЯДцдкЕуBЃЌЕуAЁЂBЕФЁАСьгђЁБЕФУцЛ§ВЛГЌЙ§16ЃЌжБНгаДГіmЕФШЁжЕЗЖЮЇЃЎ
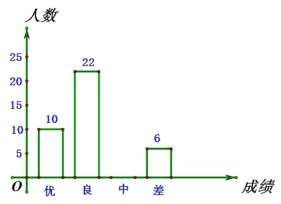
ЁОД№АИЁПЃЈ1ЃЉ40ЃЛЃЈ2ЃЉЂйBЃЈ4ЃЌ2ЃЉЛђBЃЈ0ЃЌ2ЃЉЃЛЂкЉ12ЁмmЁм4ЃЎ
ЁОНтЮіЁП
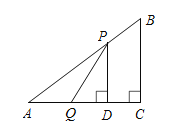
ЃЈ1ЃЉгЩСНЕуОрРыЙЋЪНПЩЧѓABГЄЃЌгЩе§ЗНаЮЕФаджЪПЩЧѓНтЃЛ
ЃЈ2ЃЉЂйЗжСНжжЧщПіЃЌгЩСНЕуОрРыЙЋЪНКЭе§ЗНаЮаджЪПЩЧѓНтЃЛ
ЂкгЩЬтвтПЩЕУBMЃНAMЃЌПЩЕУmЃН4Љ4aЃЌЛђmЃНЉ2aЃЌгЩе§ЗНаЮЕФаджЪПЩЧѓaЕФШЁжЕЗЖЮЇЃЌМДПЩЧѓНтЃЎ
ЃЈ1ЃЉЁпЕуAЕФзјБъЮЊЃЈЉ1ЃЌ1ЃЉЃЌЕуBЕФзјБъЮЊЃЈ3ЃЌ3ЃЉЃЌ
ЁрABЃН![]() ЃЌ
ЃЌ
гЩЬтвтПЩжЊЃЌABЪЧе§ЗНаЮЖдНЧЯпЕФвЛАыЃЌ
Ёре§ЗНаЮЕФБпГЄЮЊ2![]() ЃЌ
ЃЌ
Ёре§ЗНаЮЕФУцЛ§ЮЊ40ЃЌ
ЁрЖЅЕуAЁЂBЕФЁАСьгђЁБЕФУцЛ§ЮЊ40ЃЛ
ЙЪД№АИЮЊ40ЃЛ
ЃЈ2ЃЉЂйШчЭМЃЌ
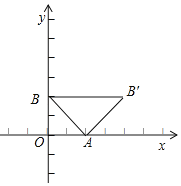
ЁпЕуAЁЂBЕФЁАСьгђЁБЕФе§ЗНаЮЕФБпгызјБъжсЦНааЛђДЙжБЃЌ
ЁрABгыxжсЕФЫљГЩШёНЧЮЊ45ЁуЃЌ
ЕБЕуBдкAзѓВрЃЌЩшBЃЈ2ЉaЃЌaЃЉЃЌ
ЁрABЃН![]() ЃЌ
ЃЌ
ЁпЕуAЁЂBЕФЁАСьгђЁБЕФУцЛ§ЮЊ16ЃЌ
Ёр16ЃН![]() ЃЌ
ЃЌ
ЁрaЃН2ЃЌ
ЁрЕуBЃЈ0ЃЌ2ЃЉЃЌ
ЕБЕуBдкЕуAгвВрЃЌЩшB'ЃЈ2+aЃЌaЃЉ
ЁрAB'ЃН![]() aЃЌ
aЃЌ
ЁпЕуAЁЂBЕФЁАСьгђЁБЕФУцЛ§ЮЊ16ЃЌ
Ёр16ЃН![]() ЃЌ
ЃЌ
ЁрaЃН2ЃЌ
ЁрЕуBЃЈ4ЃЌ2ЃЉЃЌ
злЩЯЫљЪіЃКBЃЈ4ЃЌ2ЃЉЛђBЃЈ0ЃЌ2ЃЉЃЛ
ЂкШчЭМ2ЃЌЙ§ЕуBзїBMЁЭAMЃЌ
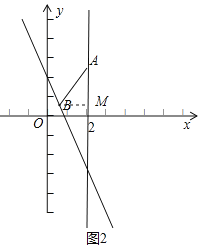
ЁпЁпЕуAЁЂBЕФЁАСьгђЁБЕФе§ЗНаЮЕФБпгызјБъжсЦНааЛђДЙжБЃЌ
ЁрABгыжБЯпxЃН2ЕФЫљГЩШёНЧЮЊ45ЁуЃЌ
ЁрBMЃНAMЃЌ
ЩшЕуBЃЈaЃЌЉ3a+2ЃЉЃЌ
ЁрAMЃН|m+3aЉ2|ЃЌBMЃН|2Љa|
ЁрABЃН![]() |2Љa|ЃЌ
|2Љa|ЃЌ
ЁпЕуAЁЂBЕФЁАСьгђЁБЕФУцЛ§ВЛГЌЙ§16ЃЌ
Ёр![]() Ём16
Ём16
Ёр0ЁмaЁм4ЃЌ
ЁпBMЃНAMЃЌ
Ёр|m+3aЉ2|ЃН|2Љa|
ЁрmЃН4Љ4aЃЌЛђmЃНЉ2aЃЌ
ЁрЉ12ЁмmЁм4ЃЌЛђЉ8ЁмmЁм0ЃЌ
злЩЯЫљЪіЃКЉ12ЁмmЁм4ЃЎ

 МЦЫуИпЪжЯЕСаД№АИ
МЦЫуИпЪжЯЕСаД№АИ