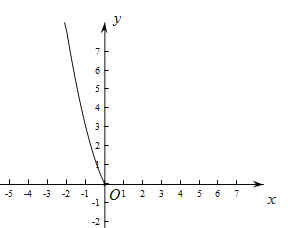题目内容
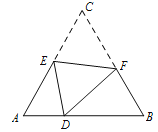
【题目】如图，D是等边△ABC边AD上的一点，且AD：DB=1：2，现将△ABC折叠，使点C与D重合，折痕为EF，点E、F分别在AC、BC上，则CE：CF=（ ）
A、
B、
C、
D、
【答案】B.
【解析】
试题由折叠的性质可得，∠EDF=∠C=60,CE=DE,CF=DF.再由∠BDF+∠ADE=∠BDF+∠BFD=120,可得∠ADE=∠BFD，又因∠A=∠B=60，根据两角对应相等的两三角形相似可得△AED∽△BDF,所以
，设AD=a，BD=2a，AB=BC=CA=3a，再设CE==DE=x，CF==DF=y，则AE=3a-x，BF=3a-y，
所以
，整理可得ay=3ax-xy，2ax=3ay-xy，即xy=3ax-ay①，xy=3ay-2ax②；把①代入②可得3ax-ay=3ay-2ax，所以5ax=4ay，
，即
,故答案选B.
练习册系列答案
相关题目
【题目】甲、乙两人在5次打靶测试中命中的环数如下：
甲：8，8，7，8，9
乙：5，9，7，10，9
（1）填写下表：
平均数 | 众数 | 中位数 | 方差 | |
甲 | 8 | | 8 | 0.4 |
乙 | | 9 | | 3.2 |
（2）教练根据这5次成绩，选择甲参加射击比赛，教练的理由是什么？
（3）如果乙再射击1次，命中8环，那么乙的射击成绩的方差 ．（填“变大”、“变小”或“不变”）．
【题目】探究函数
的图象与性质.
(1)下表是y与x的几组对应值.
| … |
|
|
|
|
|
|
| … |
| … |
|
|
|
|
|
|
| … |
其中m的值为_______________；
(2)根据上表数据，在如图所示的平面直角坐标系中描点，并已画出了函数图象的一部分，请你画出该图象的另一部分；
(3)结合函数的图象，写出该函数的一条性质：_____________________________；
(4)若关于x的方程
有2个实数根，则t的取值范围是___________________.
