题目内容
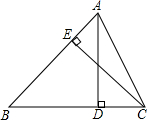
某兴趣小组在学习了勾股定理之后提出:“锐(钝)角三角形有没有类似于勾股定理的结论”的问题.首先定义了一个新的概念:如图(1)△ABC中,M是BC的中点,P是射线MA上的点,设
=k,若∠BPC=90°,则称k为勾股比.

(1)如图(1),过B、C分别作中线AM的垂线,垂足为E、D.求证:CD=BE.
(2)①如图(2),当=1,且AB=AC时,AB2+AC2=______BC2(填一个恰当的数).
②如图(1),当k=1,△ABC为锐角三角形,且AB≠AC时,①中的结论还成立吗?若成立,请写出证明过程;若不成立,也请说明理由;
③对任意锐角或钝角三角形,如图(1)、(3),请用含勾股比k的表达式直接表示AB2+AC2与BC2的关系(写出锐角或钝角三角形中的一个即可).
| AP |
| PM |

(1)如图(1),过B、C分别作中线AM的垂线,垂足为E、D.求证:CD=BE.
(2)①如图(2),当=1,且AB=AC时,AB2+AC2=______BC2(填一个恰当的数).
②如图(1),当k=1,△ABC为锐角三角形,且AB≠AC时,①中的结论还成立吗?若成立,请写出证明过程;若不成立,也请说明理由;
③对任意锐角或钝角三角形,如图(1)、(3),请用含勾股比k的表达式直接表示AB2+AC2与BC2的关系(写出锐角或钝角三角形中的一个即可).
(1)证明:∵M是BC的中点,
∴BM=CM,
∵BE⊥AM于E,CD⊥AM于D,
∴∠E=∠CDM=90°,
在△BME和△CMD中,
,
∴△BME≌△CMD(AAS),
∴CD=BE;
(2)①AB2+AC2=2.5BC2.
理由如下:∵AM是△ABC的中线,
∴PM=BM=CM=
BC,
∵k=1,
∴AP=PM,
∴AM=2PM=BC,
在Rt△ABM中,AB2=AM2+BM2=BC2+
BC2=
BC2,
在Rt△ACM中,AC2=AM2+CM2=BC2+
BC2=
BC2,
∴AB2+AC2=
BC2+
BC2=2.5BC2;
即AB2+AC2=2.5BC2;
②结论仍然成立.
设EM=DM=a,则AE=AM+a,AD=AM-a,
在Rt△ABE中,AB2=AE2+BE2=(AM+a)2+BE2=AM2+2AM•a+a2+BE2,
在Rt△ACD中,AC2=AD2+CD2=(AM-a)2+CD2=AM2-2AM•a+a2+CD2,
∴AB2+AC2=2AM2+(a2+BE2)+(a2+CD2),
∵BE⊥AM于E,CD⊥AM于D,
∴∠E=∠CDM=90°,
∴a2+BE2=BM2=
BC2,a2+CD2=CM2=
BC2,
∴AB2+AC2=2AM2+
BC2,
∵
=1,
∴AP=PM,
∵∠BPC=90°,AM是△ABC的中线,
∴PM=
BC,
若△ABC是锐角三角形,则AM=AP+PM=PM+PM=(1+1)PM=BC,
∴AB2+AC2=2×BC2+
BC2=
BC2,
即AB2+AC2=2.5BC2;
③结论:锐角三角形:AB2+AC2=
BC2,
钝角三角形:AB2+AC2=
BC2,
理由如下:设EM=DM=a,则AE=AM+a,AD=AM-a,
在Rt△ABE中,AB2=AE2+BE2=(AM+a)2+BE2=AM2+2AM•a+a2+BE2,
在Rt△ACD中,AC2=AD2+CD2=(AM-a)2+CD2=AM2-2AM•a+a2+CD2,
∴AB2+AC2=2AM2+(a2+BE2)+(a2+CD2),
∵BE⊥AM于E,CD⊥AM于D,
∴∠E=∠CDM=90°,
∴a2+BE2=BM2=
BC2,a2+CD2=CM2=
BC2,
∴AB2+AC2=2AM2+
BC2,
∵
=k,
∴AP=kPM,
∵∠BPC=90°,AM是△ABC的中线,
∴PM=
BC,
若△ABC是锐角三角形,则AM=AP+PM=kPM+PM=(k+1)PM=
BC,
∴AB2+AC2=2×(
BC)2+
BC2=
BC2,
即AB2+AC2=
BC2;
若△ABC是钝角三角形,则AM=PM+AP=PM-kPM=(1-k)PM=
BC,
AB2+AC2=2×(
BC)2+
BC2=
BC2,
即AB2+AC2=
BC2.
∴BM=CM,
∵BE⊥AM于E,CD⊥AM于D,
∴∠E=∠CDM=90°,
在△BME和△CMD中,
|
∴△BME≌△CMD(AAS),
∴CD=BE;
(2)①AB2+AC2=2.5BC2.
理由如下:∵AM是△ABC的中线,
∴PM=BM=CM=
| 1 |
| 2 |
∵k=1,
∴AP=PM,
∴AM=2PM=BC,
在Rt△ABM中,AB2=AM2+BM2=BC2+
| 1 |
| 4 |
| 5 |
| 4 |
在Rt△ACM中,AC2=AM2+CM2=BC2+
| 1 |
| 4 |
| 5 |
| 4 |
∴AB2+AC2=
| 5 |
| 4 |
| 5 |
| 4 |
即AB2+AC2=2.5BC2;
②结论仍然成立.
设EM=DM=a,则AE=AM+a,AD=AM-a,
在Rt△ABE中,AB2=AE2+BE2=(AM+a)2+BE2=AM2+2AM•a+a2+BE2,
在Rt△ACD中,AC2=AD2+CD2=(AM-a)2+CD2=AM2-2AM•a+a2+CD2,
∴AB2+AC2=2AM2+(a2+BE2)+(a2+CD2),
∵BE⊥AM于E,CD⊥AM于D,
∴∠E=∠CDM=90°,
∴a2+BE2=BM2=
| 1 |
| 4 |
| 1 |
| 4 |
∴AB2+AC2=2AM2+
| 1 |
| 2 |
∵
| AP |
| PM |
∴AP=PM,
∵∠BPC=90°,AM是△ABC的中线,
∴PM=
| 1 |
| 2 |
若△ABC是锐角三角形,则AM=AP+PM=PM+PM=(1+1)PM=BC,
∴AB2+AC2=2×BC2+
| 1 |
| 2 |
| 5 |
| 2 |
即AB2+AC2=2.5BC2;
③结论:锐角三角形:AB2+AC2=
| k2+2k+2 |
| 2 |
钝角三角形:AB2+AC2=
| k2-2k+2 |
| 2 |
理由如下:设EM=DM=a,则AE=AM+a,AD=AM-a,
在Rt△ABE中,AB2=AE2+BE2=(AM+a)2+BE2=AM2+2AM•a+a2+BE2,
在Rt△ACD中,AC2=AD2+CD2=(AM-a)2+CD2=AM2-2AM•a+a2+CD2,
∴AB2+AC2=2AM2+(a2+BE2)+(a2+CD2),
∵BE⊥AM于E,CD⊥AM于D,
∴∠E=∠CDM=90°,
∴a2+BE2=BM2=
| 1 |
| 4 |
| 1 |
| 4 |
∴AB2+AC2=2AM2+
| 1 |
| 2 |
∵
| AP |
| PM |
∴AP=kPM,
∵∠BPC=90°,AM是△ABC的中线,
∴PM=
| 1 |
| 2 |
若△ABC是锐角三角形,则AM=AP+PM=kPM+PM=(k+1)PM=
| k+1 |
| 2 |
∴AB2+AC2=2×(
| k+1 |
| 2 |
| 1 |
| 2 |
| k2+2k+2 |
| 2 |
即AB2+AC2=
| k2+2k+2 |
| 2 |
若△ABC是钝角三角形,则AM=PM+AP=PM-kPM=(1-k)PM=
| 1-k |
| 2 |
AB2+AC2=2×(
| 1-k |
| 2 |
| 1 |
| 2 |
| k2-2k+2 |
| 2 |
即AB2+AC2=
| k2-2k+2 |
| 2 |

练习册系列答案
相关题目