题目内容
【题目】如图，点A、B、D、E在⊙O上，弦AE、BD的延长线相交于点C．若AB是⊙O的直径，D是BC的中点． 
（1）试判断AB、AC之间的大小关系，并给出证明；
（2）在上述题设条件下，当△ABC为正三角形时，点E是否AC的中点？为什么？
【答案】
（1）AB=AC，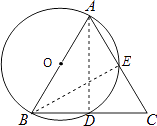 
证明：连结AD，
∵AB是⊙O的直径
∴∠ADB=90°，
即AD⊥BC，
∵BD=DC，
∴AB=AC
（2）解：当△ABC为正三角形时，E是AC的中点，
连接BE，
∵AB为直径，
∴∠BEA=90°，
即BE⊥AC，
∵△ABC为正三角形，
∴AE=EC，
即E是AC的中点
【解析】（1）连接AD，根据圆周角定理求出∠ADB=90°，根据线段垂直平分线性质推出即可；（2）根据圆周角定理求出∠AEB=90°，根据等腰三角形性质求出即可．
练习册系列答案
相关题目
