题目内容
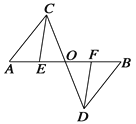
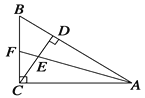
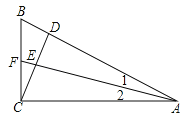
【题目】如图,在△ABC中,∠ACB=90°,CD是AB边上的高,∠BAC的平分线为AF,AF与CD交于点E,则△CEF是__________三角形.
【答案】等腰
【解析】
首先根据条件∠ACB=90°,CD是AB边上的高,可证出∠BCD+∠ACD=90°,∠B+∠BCD=90°,再根据同角的补角相等可得到∠B=∠DCA,再利用三角形的外角与内角的关系可得到∠CFE=∠FEC,最后利用等角对等边可证出结论.
∵∠ACB=90°,∴∠BCD+∠ACD=90°.
∵CD是AB边上的高,∴∠B+∠BCD=90°,∴∠B=∠DCA.
∵AF是∠BAC的平分线,∴∠1=∠2.
∵∠1+∠B=∠CFE,∠2+∠DCA=∠FEC,∴∠CFE=∠FEC,∴CF=CE,∴△CEF是等腰三角形.
故答案为:等腰.

练习册系列答案
相关题目