Ő‚ńŅńŕ»›
°ĺŐ‚ńŅ°Ņ2018ńÍ Ó∆ŕŃŔĹŁ£¨—ß…ķ√«“≤Ņ…«Šň…ĻšĻš…Ő≥°£¨—°‘Ů◊‘ľļ–ń“«Ķń“¬∑Ģ![]() į≤‘ņ…ŌłģĹ÷“Ľ∑Ģ◊įĶÍņŌįŚīÚň„≤ĽīŪ ß’‚“ĽŃľĽķ£¨ľ∆ĽģĻļĹÝľ◊°Ę““ŃĹ÷÷T–Ű
į≤‘ņ…ŌłģĹ÷“Ľ∑Ģ◊įĶÍņŌįŚīÚň„≤ĽīŪ ß’‚“ĽŃľĽķ£¨ľ∆ĽģĻļĹÝľ◊°Ę““ŃĹ÷÷T–Ű![]() “—÷™ĻļĹÝľ◊T–Ű2ľĢļÕ““T–Ű3ľĢĻ≤–Ť310‘™£ĽĻļĹÝľ◊T–Ű1ľĢļÕ““T–Ű2ľĢĻ≤–Ť190‘™
“—÷™ĻļĹÝľ◊T–Ű2ľĢļÕ““T–Ű3ľĢĻ≤–Ť310‘™£ĽĻļĹÝľ◊T–Ű1ľĢļÕ““T–Ű2ľĢĻ≤–Ť190‘™
![]() «ůľ◊°Ę““ŃĹ÷÷T–Ű√ŅľĢĶńĹÝľŘ∑÷Īū «∂ŗ…Ŕ‘™£Ņ
«ůľ◊°Ę““ŃĹ÷÷T–Ű√ŅľĢĶńĹÝľŘ∑÷Īū «∂ŗ…Ŕ‘™£Ņ
![]() ő™¬ķ◊„ –≥°–Ť«ů£¨∑Ģ◊įĶÍ–ŤĻļĹÝľ◊°Ę““ŃĹ÷÷T–ŰĻ≤100ľĢ£¨“™«ůĻļ¬ÚŃĹ÷÷T–ŰĶń◊‹∑—”√≤Ľ≥¨Ļż6540‘™£¨≤Ę«“Ļļ¬Úľ◊T–ŰĶń żŃŅ”¶–°”ŕĻļ¬Úľ◊““ŃĹ÷÷T–Ű◊‹ żŃŅĶń
ő™¬ķ◊„ –≥°–Ť«ů£¨∑Ģ◊įĶÍ–ŤĻļĹÝľ◊°Ę““ŃĹ÷÷T–ŰĻ≤100ľĢ£¨“™«ůĻļ¬ÚŃĹ÷÷T–ŰĶń◊‹∑—”√≤Ľ≥¨Ļż6540‘™£¨≤Ę«“Ļļ¬Úľ◊T–ŰĶń żŃŅ”¶–°”ŕĻļ¬Úľ◊““ŃĹ÷÷T–Ű◊‹ żŃŅĶń![]() £¨«Žń„Õ®Ļżľ∆ň„£¨»∑∂®∑Ģ◊įĶÍĻļ¬Úľ◊““ŃĹ÷÷T–ŰĶńĻļ¬Ú∑Ĺįł£ģ
£¨«Žń„Õ®Ļżľ∆ň„£¨»∑∂®∑Ģ◊įĶÍĻļ¬Úľ◊““ŃĹ÷÷T–ŰĶńĻļ¬Ú∑Ĺįł£ģ
°ĺīūįł°Ņ(1) ľ◊÷÷T–Ű√ŅľĢĹÝľŘő™50‘™£¨““÷÷T–Ű√ŅľĢĹÝľŘő™70‘™;(2)ľŻĹ‚őŲ.
°ĺĹ‚őŲ°Ņ
(1)…Ťľ◊÷÷…Ő∆∑√ŅľĢĶńĹÝľŘő™x‘™£¨““÷÷…Ő∆∑√ŅľĢĶńĹÝľŘő™y‘™£¨łýĺ›°įĻļĹÝľ◊…Ő∆∑2ľĢļÕ““…Ő∆∑3ľĢĻ≤–Ť270‘™£ĽĻļĹÝľ◊…Ő∆∑3ľĢļÕ““…Ő∆∑2ľĢĻ≤–Ť230‘™°ĪŅ…Ń–≥ŲĻō”ŕx°ĘyĶń∂Ģ‘™“Ľīő∑Ĺ≥Ő◊ť£¨Ĺ‚∑Ĺ≥Ő◊ťľīŅ…Ķ√≥ŲŃĹ÷÷…Ő∆∑ĶńĶ•ľŘ£Ľ(2)…Ť…Ő≥°ĻļĹÝľ◊÷÷T–ŰaľĢ£¨‘ÚĻļĹÝ““÷÷T–Űő™(100-a)ľĢ.łýĺ›°įĻļ¬ÚŃĹ÷÷T–ŰĶń◊‹∑—”√≤Ľ≥¨Ļż6540‘™£¨≤Ę«“Ļļ¬Úľ◊T–ŰĶń żŃŅ”¶–°”ŕĻļ¬Úľ◊““ŃĹ÷÷T–Ű◊‹ żŃŅĶń![]() °ĪŃ–≥Ų≤ĽĶ» Ĺ◊ť≤ĘĹ‚īū£ģ
°ĪŃ–≥Ų≤ĽĶ» Ĺ◊ť≤ĘĹ‚īū£ģ
![]() …Ťľ◊÷÷T–Ű√ŅľĢĹÝľŘő™x‘™£¨““÷÷T–Ű√ŅľĢĹÝľŘő™y‘™
…Ťľ◊÷÷T–Ű√ŅľĢĹÝľŘő™x‘™£¨““÷÷T–Ű√ŅľĢĹÝľŘő™y‘™![]() ”…Ő‚“‚Ķ√
”…Ő‚“‚Ķ√![]()
Ĺ‚Ķ√![]()
īū£ļľ◊÷÷T–Ű√ŅľĢĹÝľŘő™50‘™£¨““÷÷T–Ű√ŅľĢĹÝľŘő™70‘™£ģ![]() …Ť…Ő≥°ĻļĹÝľ◊÷÷T–ŰaľĢ£¨‘ÚĻļĹÝ““÷÷T–Űő™
…Ť…Ő≥°ĻļĹÝľ◊÷÷T–ŰaľĢ£¨‘ÚĻļĹÝ““÷÷T–Űő™![]() ľĢ£ģ
ľĢ£ģ
łýĺ›Ő‚“‚Ķ√£ļ
Ĺ‚Ķ√![]()
![]() ő™’Ż ż£¨
ő™’Ż ż£¨![]() ő™23ĽÚ24
ő™23ĽÚ24![]() ĶĪ
ĶĪ![]() Ī£¨
Ī£¨![]() £Ľ
£Ľ
ĶĪ![]() Ī£¨
Ī£¨![]()
![]() ”–ŃĹ÷÷Ļļ¬Ú∑Ĺįł£¨∑Ĺįł“Ľ£ļĻļ¬Úľ◊÷÷T–Ű23ľĢ£¨Ļļ¬Ú““÷÷T–Ű77ľĢ£¨
”–ŃĹ÷÷Ļļ¬Ú∑Ĺįł£¨∑Ĺįł“Ľ£ļĻļ¬Úľ◊÷÷T–Ű23ľĢ£¨Ļļ¬Ú““÷÷T–Ű77ľĢ£¨
∑Ĺįł∂Ģ£ļĻļ¬Úľ◊÷÷T–Ű24ľĢ£¨Ļļ¬Ú““÷÷T–Ű76ľĢ£ģ

 ŐžŐžŌÚ…Ō“ĽĪĺļ√ĺŪŌĶŃ–īūįł
ŐžŐžŌÚ…Ō“ĽĪĺļ√ĺŪŌĶŃ–īūįł –°—ß…ķ10∑÷÷””¶”√Ő‚ŌĶŃ–īūįł
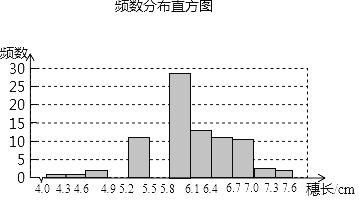
–°—ß…ķ10∑÷÷””¶”√Ő‚ŌĶŃ–īūįł°ĺŐ‚ńŅ°Ņő™ŃňŅľ≤žń≥÷÷īů¬ůŌł≥§Ķń∑÷≤ľ«ťŅŲ£¨‘ŕ“ĽŅť ‘—ťŐÔņÔ≥ť»°Ńň≤Ņ∑÷¬ůňŽ£ģ≤‚Ķ√ňŁ√«Ķń≥§∂»£¨ żĺ›’ŻņŪļůĶń∆Ķ ż∑÷≤ľĪŪľį∆Ķ ż∑÷÷Ī∑ĹÕľ»ÁŌ¬£ģłý囓‘Ō¬–ŇŌĘ£¨Ĺ‚īūŌ¬Ń–ő Ő‚£ļ
ňŽ≥§x | ∆Ķ ż |
4.0°‹x£ľ4.3 | 1 |
4.3°‹x£ľ4.6 | 1 |
4.6°‹x£ľ4.9 | 2 |
4.9°‹x£ľ5.2 | 5 |
5.2°‹x£ľ5.5 | 11 |
5.5°‹x£ľ5.8 | 15 |
5.8°‹x£ľ6.1 | 28 |
6.1°‹x£ľ6.4 | 13 |
6.4°‹x£ľ6.7 | 11 |
6.7°‹x£ľ7.0 | 10 |
7.0°‹x£ľ7.3 | 2 |
7.3°‹x£ľ7.6 | 1 |
£®ĘŮ£©≤Ļ»ę÷Ī∑ĹÕľ£Ľ
£®ĘÚ£©Ļ≤≥ť»°Ńň¬ůňŽ°° °°Ņ√£Ľ
£®Ęů£©∆Ķ ż∑÷≤ľĪŪĶń◊ťĺŗ «°° °°£¨◊ť ż «°° °°£Ľ
£®ĘŰ£©¬ůňŽ≥§∂»‘ŕ5.8°‹x£ľ6.1∑∂őßńŕ¬ůňŽ”–∂ŗ…ŔŅ√£Ņ’ľ≥ť»°¬ůňŽĶńįŔ∑÷÷ģľł£Ņ