题目内容
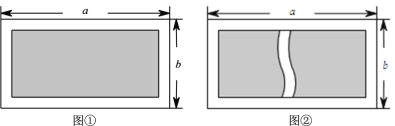
【题目】如图①,有一块长为![]() 米、宽为
米、宽为![]() 米的长方形空地,现计划将这块空地四周均留出2米宽修道路,中间用来绿化.
米的长方形空地,现计划将这块空地四周均留出2米宽修道路,中间用来绿化.
(1)求绿化的面积(用含![]() 、
、![]() 的代数式表示).
的代数式表示).
(2)若长方形空地的面积为576米2,周长为120米,求绿化的面积.
(3)若在图①的绿化部分再修一条2米宽道路,如图②,求绿化的面积(用含![]() 、
、![]() 的代数式表示).
的代数式表示).
【答案】(1)绿化的面积为![]() 米2 ;(2)绿化的面积为352米2;(3)绿化的面积为
米2 ;(2)绿化的面积为352米2;(3)绿化的面积为![]() 米2.
米2.
【解析】
(1)先用含a、b的代数式表示出绿化部分的长与宽,再根据整式的乘法法则计算;
(2)由题意,得ab=576,2(a+b)=120,然后整体代入(1)中的代数式计算即可;
(3)用含a、b的代数式分别表示出绿化部分的长与宽,再根据整式的乘法法则计算即可.
解:(1)![]() 米2,
米2,
∴绿化的面积为![]() 米2 ;
米2 ;
(2)由题意,得ab=576,2(a+b)=120,
∴ab-4a-4b+16=ab-4(a+b)+16=576-2×120+16=352(米2),
∴绿化的面积为352米2;
(3)![]() 米2.
米2.
∴绿化的面积为![]() 米2.
米2.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】探究函数![]() 的图象与性质,下面是探究过程,请补充完整:
的图象与性质,下面是探究过程,请补充完整:
(![]() )下表是
)下表是![]() 与
与![]() 的几组对应值.
的几组对应值.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
函数![]() 的自变量
的自变量![]() 的取值范围是__________,
的取值范围是__________, ![]() 的值为__________.
的值为__________.
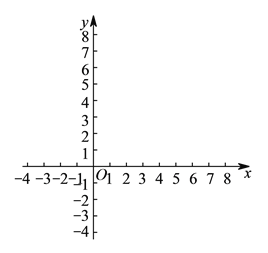
(![]() )描出以上表中各对对应值为坐标的点,并画出该函数的大致图象.
)描出以上表中各对对应值为坐标的点,并画出该函数的大致图象.
(![]() )进一步探究函数图象发现:
)进一步探究函数图象发现:
①函数图象与![]() 轴有__________个交点,所以对应方程
轴有__________个交点,所以对应方程![]() 有__________个实数根.
有__________个实数根.
②方程![]() 有__________个实数根.
有__________个实数根.
③结合函数的图象,写出该函数的一条性质__________.