题目内容
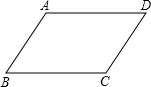
如图，ABCD为任意四边形，E、F、G、H依次为各边中点．
证明：四边形EFGH为平行四边形．
证明：四边形EFGH为平行四边形．
证明：连接BD，
∵E、H为中点，
∴EH
BD（三角形中位线定理）．
又F、G为中点，
∴FG
BD（三角形中位线定理）．
∴EH
FG．
∴四边形EFGH为平行四边形．
∵E、H为中点，
∴EH
| ||
| . |
| 1 |
| 2 |
又F、G为中点，
∴FG
| ||
| . |
| 1 |
| 2 |
∴EH
| ||
| . |
∴四边形EFGH为平行四边形．
练习册系列答案
阅读快车系列答案
相关题目
