题目内容
(2011•绍兴县模拟)如图,直线AB经过⊙O上的点C,并且OA=OB,CA=CB,⊙O交直线OB于E,D,交OA于点F,连 接EF并延长EF交AB于G,且EG⊥AB.
接EF并延长EF交AB于G,且EG⊥AB.
(1)求证:直线AB是⊙O的切线;
(2)若EF=2FG,AB=12
,求图中阴影部分的面积;
(3)若EG=9,BG=12,求BD的长.
 接EF并延长EF交AB于G,且EG⊥AB.
接EF并延长EF交AB于G,且EG⊥AB.(1)求证:直线AB是⊙O的切线;
(2)若EF=2FG,AB=12
| 3 |
(3)若EG=9,BG=12,求BD的长.
分析:(1)连接OE,由OA=OB,CA=CB,根据等腰三角形的性质得到OC⊥AB,根据切线的判定定理即可得到结论;
(2)过O点作OH⊥EG于H,则EH=FH,由EF=2FG,得到EH=
EG,又OH∥BG,根据平行线分线段成比例定理得到EH:EG=EO:EB,BO=2OE,则OB=2OC,得到∠B=30°,而BC=
AB=6
,利用含30°的直角三角形三边的关系得到OC=
BC=6,然后根据三角形和扇形的面积公式利用S阴影部分=S△OAB-S扇形OFD计算即可;
(3)利用勾股定理得到BE=
=15,易证Rt△BOC∽Rt△BEG,则OC:EG=BC:BG=BO:BE,即r:9=BC:12=BO:15,得到BC=
r,BO=
r,则15-r=
r,求出r,利用BD=BE-ED计算即可.
(2)过O点作OH⊥EG于H,则EH=FH,由EF=2FG,得到EH=
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
| ||
| 3 |
(3)利用勾股定理得到BE=
| 122+92 |
| 4 |
| 3 |
| 5 |
| 3 |
| 5 |
| 3 |
解答: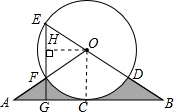 (1)证明:连接OC,如图,
(1)证明:连接OC,如图,
∵OA=OB,CA=CB,
∴OC⊥AB,
∴直线AB是⊙O的切线;
(2)解:过O点作OH⊥EG于H,如图,
∵OE=OF,
∴EH=FH,
∵EF=2FG,
∴EH=
EG,
而EG⊥AB,
∴OH∥BG,
∴EH:EG=EO:EB,
∴BO=2OE,
∴OB=2OC,
∴∠B=30°,∠COB=60°
而BC=
AB=6
,
∴OC=
BC=6,
∴S阴影部分=S△OAB-S扇形OFD
=
•12
•6-
=36
-12π;
(3)解:在Rt△BEG中,EG=9,BG=12,
∴BE=
=15,
设⊙O的半径为r,则OB=15-r,
∵OC∥EG,
∴Rt△BOC∽Rt△BEG,
∴OC:EG=BC:BG=BO:BE,即r:9=BC:12=BO:15,
∴BC=
r,BO=
r,
∴15-r=
r,解得r=
,
∴BD=BE-ED=15-2×
=
.
 (1)证明:连接OC,如图,
(1)证明:连接OC,如图,∵OA=OB,CA=CB,
∴OC⊥AB,
∴直线AB是⊙O的切线;
(2)解:过O点作OH⊥EG于H,如图,
∵OE=OF,
∴EH=FH,
∵EF=2FG,
∴EH=
| 1 |
| 3 |
而EG⊥AB,
∴OH∥BG,
∴EH:EG=EO:EB,
∴BO=2OE,
∴OB=2OC,
∴∠B=30°,∠COB=60°
而BC=
| 1 |
| 2 |
| 3 |
∴OC=
| ||
| 3 |
∴S阴影部分=S△OAB-S扇形OFD
=
| 1 |
| 2 |
| 3 |
| 120•π•62 |
| 360 |
=36
| 3 |
(3)解:在Rt△BEG中,EG=9,BG=12,
∴BE=
| 122+92 |
设⊙O的半径为r,则OB=15-r,
∵OC∥EG,
∴Rt△BOC∽Rt△BEG,
∴OC:EG=BC:BG=BO:BE,即r:9=BC:12=BO:15,
∴BC=
| 4 |
| 3 |
| 5 |
| 3 |
∴15-r=
| 5 |
| 3 |
| 45 |
| 8 |
∴BD=BE-ED=15-2×
| 45 |
| 8 |
| 15 |
| 4 |
点评:本题考查了切线的判定定理:过半径的外端点与半径垂直的直线是圆的切线.也考查了扇形的面积公式以及三角形相似的判定与性质.

练习册系列答案
相关题目
 (2011•绍兴县模拟)如图,菱形ABCD的周长为16,以AB为一边画等边△ABE,点E、D在直线AB的同侧,在AC上找一点P,使EP+DP最小,则这个最小值为
(2011•绍兴县模拟)如图,菱形ABCD的周长为16,以AB为一边画等边△ABE,点E、D在直线AB的同侧,在AC上找一点P,使EP+DP最小,则这个最小值为

 (2011•绍兴县模拟)已知菱形OABC中,A(0,5),B(3,1),连接AC交x轴于M,线段OA上有一动点P,以每秒1个单位的速度从点O出发向线段的另一端点A运动,到点A后停止运动,运动时间为t秒,过P作PE⊥AC交AB于E,连接PB、BM(如图1)
(2011•绍兴县模拟)已知菱形OABC中,A(0,5),B(3,1),连接AC交x轴于M,线段OA上有一动点P,以每秒1个单位的速度从点O出发向线段的另一端点A运动,到点A后停止运动,运动时间为t秒,过P作PE⊥AC交AB于E,连接PB、BM(如图1)