��Ŀ����
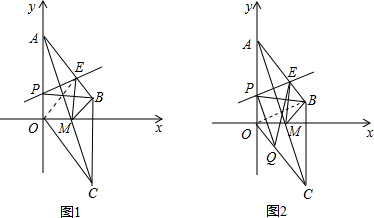
 ��2011•������ģ�⣩��֪����OABC�У�A��0��5����B��3��1��������AC��x����M���߶�OA����һ����P����ÿ��1����λ���ٶȴӵ�O�������߶ε���һ�˵�A�˶�������A��ֹͣ�˶����˶�ʱ��Ϊt�룬��P��PE��AC��AB��E������PB��BM����ͼ1��
��2011•������ģ�⣩��֪����OABC�У�A��0��5����B��3��1��������AC��x����M���߶�OA����һ����P����ÿ��1����λ���ٶȴӵ�O�������߶ε���һ�˵�A�˶�������A��ֹͣ�˶����˶�ʱ��Ϊt�룬��P��PE��AC��AB��E������PB��BM����ͼ1����1��д����C��M�����ꣻ
��2��֤����BMEΪֱ�������Σ�
��3������PB������PBM=��OAB����tan��ABP��ֵ��
��4����ͼ2�������߶�OC����һ��Q���Pͬʱ�ӵ�O����������ͬ���ٶ����C�˶������Ƿ����t��ֵ��ʹ��PQEΪ���������Σ������ڣ�����˶�ʱ�䣻�������ڣ���˵�����ɣ�
��������1��C��B�ĺ�������ȣ���C�ĺ��������B�ĺ����꣬����B��y��Ĵ�����X����ֱ�ǡ�ABX�У����ù��ɶ����������AB�ij�����BC�ij��ȿ�����ã��Ӷ����C�������ꣻ
Ȼ�����ô���ϵ�����������AC�Ľ���ʽ���������M�����ꣻ
��2������AC������OABC�ĶԳ��ᣬ���ݶԳ��Կ���֤�á�EBM=��AOM=90�����ɵõ���BME��ֱ�������Σ�
��3�����ݶԳƵ����ʣ�����֤�á�APB=90�㣬�������B�����꣮���������к����Ķ�����⣻
��4�����ݶԳƵ����ʿɵã�PE��AC�����QPB=90�㣬������PQEΪ���������Σ�ֻ�����ǣ�PE=PQ�����ݡ�APE�ס�AOB�͡�OPQ�ס�OAC����t��ʾ��PE��PQ�ij����Ӷ��õ�һ������t�ķ��̣�������⣮
Ȼ�����ô���ϵ�����������AC�Ľ���ʽ���������M�����ꣻ
��2������AC������OABC�ĶԳ��ᣬ���ݶԳ��Կ���֤�á�EBM=��AOM=90�����ɵõ���BME��ֱ�������Σ�
��3�����ݶԳƵ����ʣ�����֤�á�APB=90�㣬�������B�����꣮���������к����Ķ�����⣻
��4�����ݶԳƵ����ʿɵã�PE��AC�����QPB=90�㣬������PQEΪ���������Σ�ֻ�����ǣ�PE=PQ�����ݡ�APE�ס�AOB�͡�OPQ�ס�OAC����t��ʾ��PE��PQ�ij����Ӷ��õ�һ������t�ķ��̣�������⣮
��� �⣺��1��C��3��-4����M��
�⣺��1��C��3��-4����M��
��0����
��2����BME��ֱ�������Σ�
���ı���OABC�����Σ�
��ֱ��AC�����ĶԳ��ᣮ
��PE��AC
���P�͵�E����O���B������AC�Գƣ�
���EBM=��AOM=90�㣮
���BME��ֱ�������Σ�
��3������OE��
�ɶԳ��Եã���PBM=��EOM��
�ߡ�PBM=��OAB����APB=��AEO��
���EOM=��OAB
�ߡ�EOM+��EOA=90��
���OAB+��EOA=90��
���APB=��AEO=90�㣮
��B��3��1��
��OP=1���Ӷ�AP=4
��tan��ABP=
��
��4����ͼ2������OB��������֪��OP=OQ����POB=��QOB
��OB��PQ
���ı���OABC�����Σ�֪OB��AC��PQ��AC��
��PE��AC��
���QPE=90��
��PQEΪ���������Σ�ֻ�����ǣ�PE=PQ��
�ɡ�APE�ס�AOB�ã�PE=
��
�ɡ�OPQ�ס�OAC�ã�PQ=
��
��
=
��
��ã�t=
��
������t=
ʱ����PQE�ǵ��������Σ�
 �⣺��1��C��3��-4����M��
�⣺��1��C��3��-4����M��| 5 |
| 3 |
��2����BME��ֱ�������Σ�
���ı���OABC�����Σ�
��ֱ��AC�����ĶԳ��ᣮ
��PE��AC
���P�͵�E����O���B������AC�Գƣ�
���EBM=��AOM=90�㣮
���BME��ֱ�������Σ�
��3������OE��
�ɶԳ��Եã���PBM=��EOM��
�ߡ�PBM=��OAB����APB=��AEO��
���EOM=��OAB
�ߡ�EOM+��EOA=90��
���OAB+��EOA=90��
���APB=��AEO=90�㣮
��B��3��1��
��OP=1���Ӷ�AP=4
��tan��ABP=
| 4 |
| 3 |
��4����ͼ2������OB��������֪��OP=OQ����POB=��QOB
��OB��PQ
���ı���OABC�����Σ�֪OB��AC��PQ��AC��
��PE��AC��
���QPE=90��
��PQEΪ���������Σ�ֻ�����ǣ�PE=PQ��
�ɡ�APE�ס�AOB�ã�PE=
| ||
| 5 |
�ɡ�OPQ�ס�OAC�ã�PQ=
3
| ||
| 5 |
��
| ||
| 5 |
3
| ||
| 5 |
��ã�t=
| 5 |
| 4 |
������t=
| 5 |
| 4 |
���������⿼�������ε����ʣ���ȷӦ����������Գ�ͼ�Σ�������ԳƵ������ǽ���ؼ���

��ϰ��ϵ�д�
 �������ͬ����ϰϵ�д�
�������ͬ����ϰϵ�д�
�����Ŀ
 ��2011•������ģ�⣩��ͼ������ABCD���ܳ�Ϊ16����ABΪһ���ȱߡ�ABE����E��D��ֱ��AB��ͬ�࣬��AC����һ��P��ʹEP+DP��С���������СֵΪ
��2011•������ģ�⣩��ͼ������ABCD���ܳ�Ϊ16����ABΪһ���ȱߡ�ABE����E��D��ֱ��AB��ͬ�࣬��AC����һ��P��ʹEP+DP��С���������СֵΪ
 ��EF���ӳ�EF��AB��G����EG��AB��
��EF���ӳ�EF��AB��G����EG��AB��